天文学家测得银河系中氦的含量约为25%.有关研究表明,宇宙中氦生成的途径有两条:一是在宇宙诞生后3分钟左右生成的;二是在宇宙演化到恒星诞生后,由恒星内的氢核聚变反应生成的.
(1)把氢核聚变反应简化为4个氢核(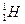
)聚变成氦核(
),同时放出2个正电子(
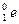)和2个中微子(ν0),请写出该氢核聚变反应的方程,并计算一次反应释放的能量.
(2)研究表明,银河系的年龄约为t=3.8×1017 s,每秒钟银河系产生的能量约为1×1037 J(即P=1×1037 J/s).现假定该能量全部来自上述氢核聚变反应,试估算银河系中氦的含量(最后结果保留一位有效数字).
(3)根据你的估算结果,对银河系中氦的主要生成途径作出判断.
(可能用到的数据:银河系质量约为M=3×1041 kg,原子质量单位1 u=1.66×10-27 kg,1 u 相当于1.5×10-10 J的能量,电子质量me="0.000" 5 u,氦核质量mα="4.002" 6 u,氢核质量mp="1.007" 8 u,中微子νe质量为零)
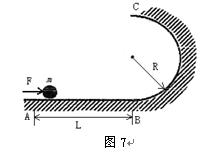
如图所示，一水平传送带始终保持着大小为v＝4m/s的速度做匀速运动。在传送带右侧有一半圆弧形的竖直放置的光滑圆弧轨道，其半径为R=0.2m，半圆弧形轨道最低点与传送带右端B衔接并相切，一小物块无初速地放到皮带左端A处，经传送带和竖直圆弧轨道至最高点C。已知当A、B之间距离为s=1m时，物块至最高点对轨道的压力为零，（g=10m/s2）则：
（1）物块至最高点C的速度为多少?
（2）物块与皮带间的动摩擦因数为多少？
（3）若只改变传送带的长度，使滑块滑至圆弧轨道的最高点C时对轨道的压力最大，传送带的长度
应满足什么条件？
一质量为m的小球以速度
水平抛出，经时间t落地，（不计空气阻力，重力加速度为g）求：
（1）此过程重力做的功；
（2）此过程中重力做功的平均功率；
（3）小球落地时重力做功的瞬时功率。
如图所示，在光滑的水平面上，一质量为m=5kg的滑块在细线的作用下，绕竖直轴以线速度v=0.4m/s做圆周运动，滑块离竖直轴的距离r=0.2m，（g=10m/s2）求：
（1）滑块运动的角速度大小；
（2）滑块受到细线拉力的大小。
如图8所示，光滑坡道顶端距水平面高度为h，质量为m的小物块A从坡道顶端由静止滑下，进入水平面上的滑道时无机械能损失，为使A制动，将轻弹簧的一端固定在水平滑道延长线M处的墙上，另一端恰位于滑道的末端O点.已知在OM段，物块A与水平面间的动摩擦因数均为μ，其余各处的摩擦不计，重力加速度为g，求：
（1）物块滑到O点时的速度大小；
（2）弹簧为最大压缩量d时的弹性势能（设弹簧处于原长时弹性势能为零）
（3）若物块A能够被弹回到坡道上，则它能够上升的最大高度是多少？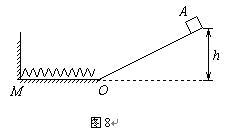
如图7所示，光滑水平面右端B处连接一个竖直的半径为R的光滑半圆固定轨道，在离B距离为L的A点，用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力，质点沿半圆轨道运动到C处后又正好落回A点。求推力对小球所做的功。