设函数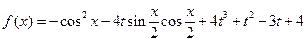 ,
,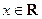 ,
,
其中|t|≤1,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)对于区间[-1,1]中的某个t,是否存在实数a,使得不等式g(t)≤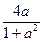 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.

某学校餐厅新推出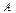 、
、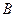 、
、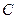 、
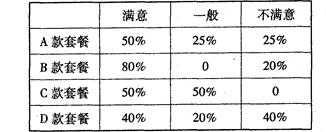
、 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:
(1)若同学甲选择的是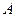 款套餐,求甲的调查问卷被选中的概率;
款套餐,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这2人中至少有一人选择的是 款套餐的概率。
款套餐的概率。
本题满分10分)
已知向量 ,
, .
.
(I)若 ,求
,求 值;
值;
(II)在 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,
,
求函数 的取值范围.
的取值范围.
(本题满分12分)
已知椭圆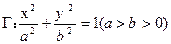 的左、右焦点为
的左、右焦点为 ,过点
,过点 斜率为正数的直线交
斜率为正数的直线交 两点,且
两点,且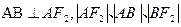 成等差数列。
成等差数列。
(Ⅰ)求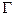 的离心率;
的离心率;
(Ⅱ)若直线y=kx(k<0)与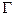 交于C、D两点,求使四边形ABCD面积S最大时k的值。
交于C、D两点,求使四边形ABCD面积S最大时k的值。
设函数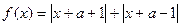 的图象关于y轴对称,函数
的图象关于y轴对称,函数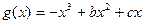 (b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(1)求f(x)的表达式;
(2)试求b的值;
(3)若 时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
(本小题满分12分)
在数列 中,已知
中,已知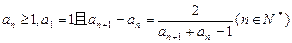
(I)求数列 的通项公式;
的通项公式;
(II)令 ,若
,若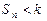 恒成立,求k的取值范围。
恒成立,求k的取值范围。