(本小题满分12分)
在数列 中,已知
中,已知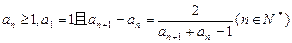
(I)求数列 的通项公式;
的通项公式;
(II)令 ,若
,若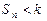 恒成立,求k的取值范围。
恒成立,求k的取值范围。
有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为0.6,
0.8,0.9.
(1)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;
(2)若四名运动员每两人之间进行一场比赛,求甲恰好胜两场的概率;
(3)若四名运动员每两人之间进行一场比赛,设甲获胜场次为 ,求随机变量
,求随机变量 的概率分布.
的概率分布.
甲、乙两人参加一次考试,已知在备选的10道试题中,甲能答对其中6题,乙能答对其中8题.若规定每次考试分别都从这10题中随机抽出3题进行测试,至少答对2题算合格.
(1)分别求甲、乙两人考试合格的概率;
(2)求甲、乙两人至少有一人合格的概率.
盒子中有10张奖券,其中3张有奖,甲、乙先后从中各抽取1张(不放回),记“甲中奖”为A,“乙中奖”为B.
(1)求P(A),P(B),P(AB),P(A|B);
(2)A与B是否相互独立,说明理由.
编号1,2,3的三位学生随意入座编号为1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的个数
是X.
(1)求随机变量X的概率分布;
(2)求随机变量X的数学期望和方差.
甲、乙两人进行投篮比赛,两人各投3球,谁投进的球数多谁获胜,已知每次投篮甲投进的概率为 ,乙投进的概率为
,乙投进的概率为 ,求:
,求:
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.