设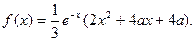
(1)求a的值,使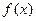 的极小值为0;
的极小值为0;
(2)证明:当且仅当a=3时,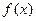 的极大值为4。
的极大值为4。
在边长为60cm的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?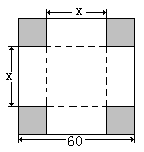
已知各项均为正数的数列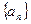 中,
中,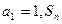 是数列
是数列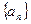 的前
的前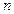 项和,对任意
项和,对任意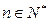 ,有
,有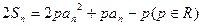
(Ⅰ)求常数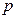 的值;
的值;
(Ⅱ)求数列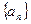 的通项公式;
的通项公式;
(Ⅲ)设数列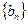 的通项公式是
的通项公式是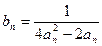 ,前
,前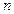 项和为
项和为 ,求证:对于任意的正整数
,求证:对于任意的正整数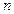 ,总有
,总有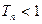 .
.
已知数列 的首项
的首项 ,
, ,
,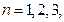 ….
….
(Ⅰ)证明:数列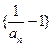 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
设p:实数x满足 ,
,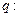 实数
实数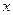 满足
满足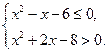 .
.
(Ⅰ)求满足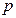 的
的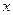 取值范围;
取值范围;
(Ⅱ)当 时,若
时,若 是
是
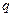 的充分不必要条件,求实数
的充分不必要条件,求实数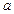 的取值范围.
的取值范围.
某化工企业2010年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(Ⅰ)求该企业使用该设备x年的年平均污水处理费用y(万元);
(Ⅱ)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?