已知各项均为正数的数列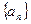 中,
中,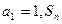 是数列
是数列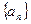 的前
的前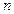 项和,对任意
项和,对任意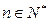 ,有
,有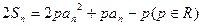
(Ⅰ)求常数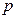 的值;
的值;
(Ⅱ)求数列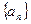 的通项公式;
的通项公式;
(Ⅲ)设数列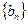 的通项公式是
的通项公式是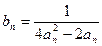 ,前
,前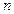 项和为
项和为 ,求证:对于任意的正整数
,求证:对于任意的正整数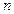 ,总有
,总有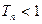 .
.
(本小题满分12分)
已知圆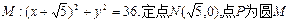 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足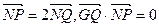 .
.
(I)求点G的轨迹C的方程;
(II)过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设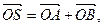 是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
(本小题满分12分)
如图,在直三棱柱 中,
中,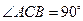 ,
,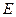 是棱
是棱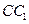 上的动点,
上的动点,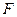 是
是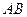 中点,
中点,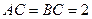 ,
,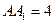 .
.
(Ⅰ)求证: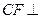 平面
平面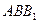 ;
;
(Ⅱ)若二面角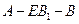 的大小是
的大小是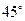 ,求
,求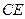 的长.
的长.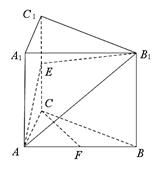
(本小题满分12分)
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示.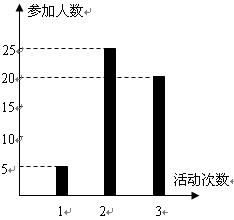
(Ⅰ)求该班学生参加活动的人均次数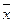 ;
;
(Ⅱ)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率;
(Ⅲ)从该班中任选两名学生,用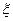 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量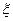 的分布列及数学期望
的分布列及数学期望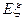 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示)
(本小题满分12分)在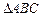 中,
中,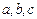 分别为角
分别为角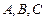 的对边,且满足
的对边,且满足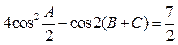
(Ⅰ)求角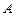 的大小;
的大小;
(Ⅱ)若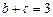 ,求
,求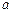 的最小值.
的最小值.
曲线C上任一点到点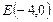 ,
,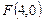 的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,
的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方, .
.
(Ⅰ)求曲线C的方程;
(Ⅱ)求点P的坐标;
(Ⅲ)以曲线C的中心为圆心,AB为直径作圆O,过点P的直线l截圆O的弦MN长为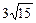 ,求直线l的方程.
,求直线l的方程.