已知函数f (x)=x3+ (1-a)x2-3ax+1,a>0.
(1-a)x2-3ax+1,a>0.
(Ⅰ) 证明:对于正数a,存在正数p,使得当x∈[0,p]时,有-1≤f (x)≤1;
(Ⅱ) 设(Ⅰ)中的p的最大值为g(a),求g(a)的最大值.
在△ABC中,AB=AC=5,BC=6,求cosB、sinA
当a>0且x>0时,因为 ,所以
,所以 ,从而
,从而 (当x=
(当x= 时取等号).记函数
时取等号).记函数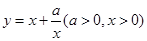 ,由上述结论可知:当x=
,由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2
(1)已知函数y1=x(x>0)与函数 ,则当x=时,y1+y2取得最小值为
,则当x=时,y1+y2取得最小值为
(2)已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>−1),求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
已知点P(1,-2a)在二次函数y=ax2+6的图象上,并且点P关于x轴的对称点在反比例函数 的图象上。
的图象上。
(1)求此二次函数和反比例函数的解析式;
(2)点(-1,4)是否同时在(1)中的两个函数图象上?
设函数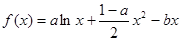 ,
,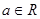 且
且 .曲线
.曲线 在点
在点 处的切线的斜率为0.
处的切线的斜率为0.
(1)求 的值;
的值;
(2)若存在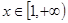 ,使得
,使得 ,求
,求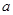 的取值范围.
的取值范围.