在锐角三角形ABC中，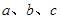
分别是角A、B、C的对边，且
．
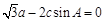（Ⅰ）求角C的大小；
（Ⅱ）若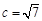
，且△ABC 的面积为
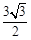，求
的值.
（本小题满分12分）
如图所示，在正方体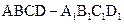
中，E是棱
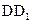的中点.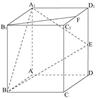
（Ⅰ）求直线BE与平面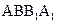
所成的角的正弦值；
（Ⅱ）在棱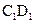
上是否存在一点F，使
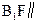平面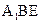
？证明你的结论.
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD,AP=AB=2,BC=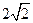
，E，F分别是AD，PC的中点.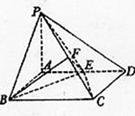 
（Ⅰ）证明：PC⊥平面BEF；
（Ⅱ）求平面BEF与平面BAP夹角的大小.
（本小题满分12分）
如图，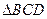
与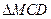
都是边长为2的正三角形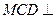，平面
平面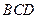
，
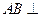平面BCD，
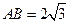．求点A到平面MBC的距离。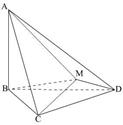
（本小题满分12分）
某医院有内科医生12名，外科医生8名，现要选派5名参加赈灾医疗队，求：
（1）某内科医生甲必须参加，某外科医生乙不能参加，有几种选法？
（2）至少有一名内科医生和至少有一名外科医生参加，有几种选法？
（本小题满分12分）
5个人排成一排，按下列要求各有多少种不同的排法？
（1）其中甲不站排头，乙不站排尾；
（2）其中甲、乙2人必须相邻；
（3）其中甲、乙2人不能相邻；
（4）其中甲、乙中间有且只有1人；
（5）其中甲只能站在乙的左侧．