(本小题满分12分)
5个人排成一排,按下列要求各有多少种不同的排法?
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙2人必须相邻;
(3)其中甲、乙2人不能相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲只能站在乙的左侧.
在 中,角
中,角 的对边分别为
的对边分别为 ,向量
,向量 ,向量
,向量 ,且
,且 :
:
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设BC中点为D,且 :求a+2c的最大值及此时
:求a+2c的最大值及此时 的面积.
的面积.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,
AE⊥BD,CB=CD=CF=1.
(1)求证:BD⊥平面AED;
(2)求B到平面FDC的距离.
如图,已知四棱锥 ,底面
,底面 为菱形,
为菱形, 平面
平面 ,
, ,
,
分别是 的中点.
的中点.
(1)证明: ;
;
(2)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
解答下列问题:
(1)求平行于直线3x+4y 2=0,且与它的距离是1的直线方程;
2=0,且与它的距离是1的直线方程;
(2)求垂直于直线x+3y 5=0,且与点P(
5=0,且与点P( 1,0)的距离是
1,0)的距离是 的直线方程.
的直线方程.
求经过点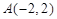 并且和
并且和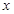 轴的正半轴、
轴的正半轴、 轴的正半轴所围成的三角形的面积是
轴的正半轴所围成的三角形的面积是 的直线方程.
的直线方程.