已知椭圆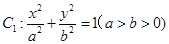 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线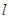 恰好与圆
恰好与圆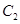 相切.
相切.
(Ⅰ)已知椭圆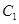 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.
(本小题满分10分)从4名男生和5名女生中任选5人参加数学课外小组,求在下列条件下各有多少种不同的选法?
(1)选2名男生和3名女生,且女生甲必须入选;
(2)至多选4名女生,且男生甲和女生乙不同时入选.
(本小题满分10分)
已知a,b,c,d∈(0,+∞),
求证ac+bd≤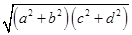 .
.
(本小题12分)如图4,四棱锥 中,底面
中,底面 是菱形,其对角线的交点为
是菱形,其对角线的交点为 ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)设 ,
, ,
, 是侧棱
是侧棱 上的一点,且
上的一点,且 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积.
已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
如图所示,正四棱锥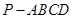 中,
中, 为底面正方形的中心,侧棱
为底面正方形的中心,侧棱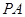 与底面
与底面 所成的角的正切值为
所成的角的正切值为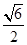 .
.
(1)求侧面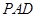 与底面
与底面 所成的二面角的大小;
所成的二面角的大小;
(2)若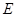 是
是 的中点,求异面直线
的中点,求异面直线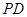 与
与 所成角的正切值;
所成角的正切值;