(本小题满分10分)选修4—4:坐标系与参数方程
已知直线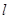 的参数方程为
的参数方程为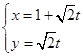 (
(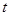 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,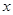 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线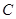 的极坐标方程是
的极坐标方程是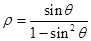 .
.
(1)写出直线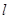 的极坐标方程与曲线
的极坐标方程与曲线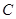 的普通方程;
的普通方程;
(2)若点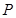 是曲线
是曲线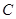 上的动点,求
上的动点,求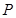 到直线
到直线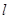 距离的最小值,并求出此时
距离的最小值,并求出此时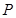 点的坐标.
点的坐标.
已知a>0且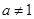 ,关于x的不等式
,关于x的不等式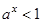 的解集是
的解集是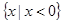 ,解关于x的不等式
,解关于x的不等式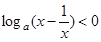 。
。
如图所示,已知圆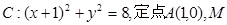 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点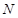 在
在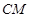 上,且满足
上,且满足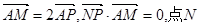 的轨迹为曲线
的轨迹为曲线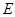 .
.
(1)求曲线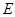 的方程;
的方程;
(2)若直线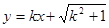 与(1)中所求点
与(1)中所求点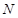 的轨迹
的轨迹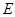 交于不同两点
交于不同两点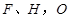 是坐标原点,且
是坐标原点,且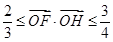 ,求△
,求△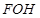 的面积的取值范围.
的面积的取值范围.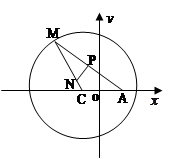
如图,在直三棱柱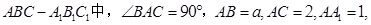
点D在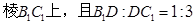
(1)证明:无论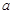 为任何正数,均有
为任何正数,均有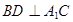 ;
;
(2)当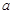 为何值时,二面角
为何值时,二面角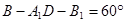 .
.
如图,三条直线 、
、 、
、 两两平行,直线
两两平行,直线 、
、 间的距离为
间的距离为 ,直线
,直线 、
、 间的距离为
间的距离为 ,
, 、
、 为直线
为直线 上的两个定点,且
上的两个定点,且 ,
, 是在直线
是在直线 上滑动的长度为
上滑动的长度为 的线段.
的线段.
(1)建立适当的平面直角坐标系,求△ 的外心
的外心 的轨迹
的轨迹 ;
;
(2)当△ 的外心
的外心 在
在 上什么位置时,使
上什么位置时,使 最小?最小值是多少?(其中,
最小?最小值是多少?(其中, 为外心
为外心 到直线
到直线 的距离)
的距离)
(12分)已知两点
 满足条件
满足条件 的动点P的轨迹是曲线
的动点P的轨迹是曲线 ,
, 与曲线
与曲线 交于
交于 、
、 两点.
两点.
(1)求k的取值范围;
(2)如果 求直线l的方程.
求直线l的方程.