如图,在直三棱柱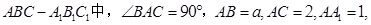
点D在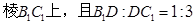
(1)证明:无论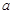 为任何正数,均有
为任何正数,均有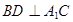 ;
;
(2)当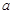 为何值时,二面角
为何值时,二面角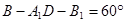 .
. 
(本小题满分12分)
已知 ,设
,设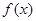 =
=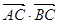 (1).求
(1).求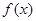 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)设关于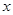 的方程
的方程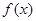 =
=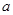 在
在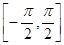 有两个不相等的实数根,求
有两个不相等的实数根,求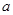 的取值范围.
的取值范围.
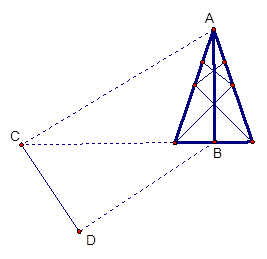
(10分) 测量河对岸的塔高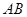 时,可以选与塔底
时,可以选与塔底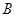 在同一水平面内的两个测点
在同一水平面内的两个测点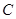 与
与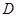 .现测得
.现测得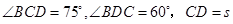 ,并在点
,并在点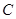 测得塔顶
测得塔顶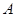 的仰角为
的仰角为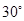 ,求塔高
,求塔高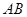 。
。
设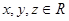 且
且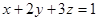 .
.
(I)当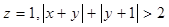 时,求实数
时,求实数 的取值范围;
的取值范围;
(II)当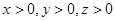 时,求
时,求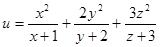 的最小值.
的最小值.
已知函数f (x )=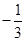 ax 3 + x2 + 2( a ≠ 0 ) .
ax 3 + x2 + 2( a ≠ 0 ) .
(Ⅰ) 试讨论函数f (x )的单调性;
(Ⅱ) 若a>0,求函数f (x ) 在[1,2]上的最大值.
在等比数列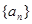 中,
中,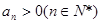 ,公比
,公比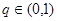 ,且
,且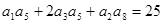 ,
,
又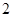 是
是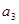 与
与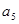 的等比中项。设
的等比中项。设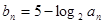 .
.
(Ⅰ) 求数列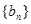 的通项公式;
的通项公式;
(Ⅱ) 已知数列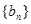 的前
的前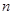 项和为
项和为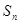 ,
,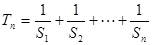 ,求
,求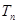 .
.