已知不等式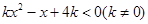 .
.
(1)若不等式的解集为
(2)若不等式的解集为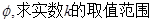 .
.
(本小题11分) 在7块大小及条件相同的试验田上施肥,做肥量对小麦产量影响的试验,得到如下一组数据:
| 施化肥量x |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
| 小麦产量 |
330 |
345 |
365 |
405 |
445 |
450 |
455 |
(1)画出散点图;
(2)对x与y进行线性回归分析,并预测施肥量30时小麦的产量为多少?
(本小题10分) 为了决定在白鼠中血糖的减少量和注射胰岛素A的剂量间的关系,将同样条件下繁殖的7只白鼠注射不同剂量的胰岛素A.所得数据如下:
| A的剂量x |
0.20 |
0.25 |
0.25 |
0.30 |
0.40 |
0.50 |
0.50 |
| 血糖减少量y |
30 |
26 |
40 |
35 |
54 |
56 |
65 |
(1)求出y对x的线性回归方程;
(2)x与y之间的线性相关关系有无统计意义(可靠性不低于95%)
某10名同学的数学、物理、语文成绩如下表:
| 数学 |
136 |
125 |
122 |
87 |
108 |
113 |
111 |
70 |
94 |
74 |
| 物理 |
107 |
91 |
92 |
76 |
93 |
85 |
82 |
78 |
78 |
73 |
| 语文 |
86 |
114 |
104 |
109 |
100 |
106 |
112 |
104 |
95 |
99 |
试分别研究他们的数学成绩与物理成绩的关系、数学成绩与语文成绩的关系,你能发现什么规律?
某大型企业人力资源部为了研究企业员工工作积极性和对企业改革态度的关系,随机抽取了189名员工进行调查,所得数据如下表所示:
| 积极支持企业改革 |
不赞成企业改革 |
合计 |
|
| 工作积极 |
54 |
40 |
94 |
| 工作一般 |
32 |
63 |
95 |
| 合计 |
86 |
103 |
189 |
对于人力资源部的研究项目,根据上述数据能得出什么结论?
在7块面积相同的试验田上进行施化肥量对水稻产量影响的试验,得到如下表所示的一组数据(单位:kg)
施化肥量 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
水稻产量 |
330 |
345 |
365 |
405 |
445 |
450 |
455 |
(1)试求 对
对 的线性回归方程;
的线性回归方程;
(2)当施化肥量 kg时,预测水稻产量.
kg时,预测水稻产量.