如图所示，水平面O点的右侧光滑，左侧粗糙．O点到右侧竖直墙壁的距离为L，一系统由可看作质点A、B两木块和一短而硬（即劲度系数很大）的轻质弹簧构成．A、B两木块的质量均为m，弹簧夹在A与B之间，与二者接触而不固连．让A、B压紧弹簧，并将它们锁定，此时弹簧的弹性势能为E0。若通过遥控解除锁定时，弹簧可瞬时恢复原长． 该系统在O点从静止开始在水平恒力F作用下开始向右运动，当运动到离墙S=L/4时撤去恒力F，撞击墙壁后以原速率反弹，反弹后当木块A运动到O点前解除锁定．求
（1）解除锁定前瞬间，A、B的速度多少？
（2）解除锁定后瞬间，A、B的速度分别为多少？
（3）解除锁定后F、L、E0、m、满足什么条件时，B具有的动能最小，这样A 能运动到距O点最远距离为多少？（A与粗糙水平面间的摩擦因数为μ）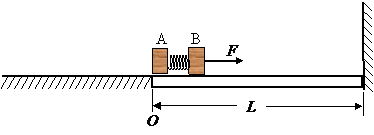
一物体做匀加速直线运动，初速度为0.5 m/s，其 7 s内的位移比5 s内的位移多25 m，
求：(1) 物体的加速度；(2) 物体在第5 s内的位移．
目前，滑板运动受到青少年的追捧。如图是某滑板运动员在一次表演时的一部分赛道在竖直平面内的示意图。赛道光滑，FGI为圆弧赛道，半径R = 6.5m，G为最低点并与水平赛道BC位于同一水平面，KA、DE平台的高度都为h = 1.8m。B、C、F处平滑连接。滑板a和b的质量均为m，m = 5kg，运动员质量为M，M = 45kg。
表演开始，运动员站在滑板b上。先让滑板a从A点静止下滑，t1=0.1s后再与b板一起从A点静止下滑。滑上BC赛道后，运动员从b板跳到同方向运动的a板上，在空中运动的时间t2 = 0.6s(水平方向是匀速运动)。运动员与a板一起沿CD赛道上滑后冲出赛道，落在EF赛道的P点，沿赛道滑行，经过G点时，运动员受到滑板a的支持力N = 742.5N。(滑板和运动员的所有运动都在同一竖直平面内，计算时滑板和运动员都看作质点，取g = 10m/s2)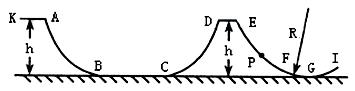
(1) 滑到G点时，运动员的速度是多大?
(2) 运动员跳上滑板a后，在BC赛道上与滑板a共同运动的速度是多大?
(3) 从表演开始到运动员滑至I的过程中，系统的机械能改变了多少？
如图所示，光滑水平面上有一质量M＝4.0kg的平板车，车的上表面右侧是一段水平轨道，水平轨道左侧连一半径R＝0.25m的1/4圆弧轨道，圆弧轨道与水平轨道在
点相切．车右端C点固定一个处于自然状态的弹簧，弹簧左端恰与水平轨道上B点相齐。一质量m＝1.0kg的小物块从圆弧形轨道顶端由静止释放，小车B部分与小物块间摩擦系数为μ＝0.2，其余各部分摩擦不计。已知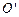B的长度L＝1m， g取10m/s2．求：
(1) 小物块经过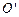点时的速度大小；
(2) 弹簧的最大弹性势能；
(3) 小物块最终离小车B点的距离。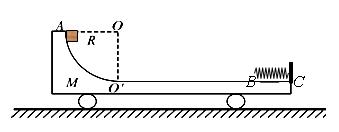
如图所示，一小物块从倾角
的斜面上的A点由静止开始滑下，最后停在水平面上的C点。已知小物块的质量m = 0.10kg，小物体与斜面和水平面间的动摩擦因数均为μ＝0.25，A点到斜面底部B点的距离L = 0.50m，斜面与水平面平滑连接，小物块滑过斜面与水平面连接处时无机械能损失。求：
(1) 小物块在斜面上运动时的加速度大小；
(2) BC间的距离；
(3) 若在C点给小物块一水平初速度使小物块恰能回到A点，此初速度为多大？（
）
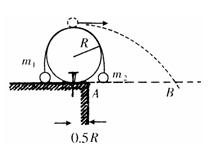
如图所示，半径为R的光滑圆柱体被固定在水平平台上，圆柱体中心离台边水平距离为0.5R，质量为m1的小球用轻绳跨过圆柱与小球m2相连，开始时将m1控制住放在平台上，两边轻绳竖直.现在释放m1，让m1和m2分别由静止开始运动，当m1上升到圆柱体的最高点时，绳子突然断了，m1恰能做平抛运动，重力加速度为g，求：
（1）m1平抛时的速度v多大？
（2）m2应为m1的多少倍？
（3）m1做平抛运动的过程中，恰能经过与台面等高的B点，求B点离台边的距离SAB多大？