利用如图14所示的装置可测量弹簧的劲度系数.一小平面镜B(可视为一点)竖直固定在物块P上,它们的总质量为m.现将P紧靠着直立的弹簧上端,用插销K固定,此时弹簧处于自然长度,从固定的点光源S发出的光经过平面镜反射后在竖直标尺的A点形成一小光斑.松开插销K,发现最终小光斑稳定在标尺上某点,该点到A点的距离为h.已知点光源S与平面镜的水平距离为L0,标尺与平面镜的水平距离为L,求该弹簧的劲度系数.
图14
如果把地球绕太阳公转看作是匀速圆周运动,轨道平均半径约为1.5×108 km,已知万有引力常量G=6.67×10-11N·m2/kg2,则可估算出太阳的质量大约是多少?(结果取一位有效数字)
如图所示,一个质量为m,电阻为R的闭合矩形线圈,长为l,高为h,从某一高度由静止开始下落,进入一个有界匀强磁场区域,磁场方向垂直纸面向里,磁感应强度大小为B,磁场的边界为水平,宽度为2h,线圈开始下落时距磁场上边界3h,下落过程中始终在竖直平面内,不发生转动.已知线圈从磁场中穿出的过程中,做的是匀速运动.求线圈在进入磁场的过程中有多少电能转化为内能?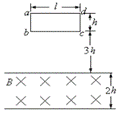
两个行星质量分别为m1和m2,绕太阳运行的轨道半径分别是r1和r2,求:
(1)它们与太阳间的万有引力之比;
(2)它们的公转周期之比.
某星球可视为球体,其自转周期为T.在它的两极处用弹簧秤测得某物体重为P,在它的赤道上用弹簧秤测得同一物体重为0.9P,星球的平均密度是多少?
在月球上以初速度v0竖直上抛一个小球,经过时间t落回到抛出点,已知月球的半径为R,试求月球的质量.