人类的陆上运输经历了从马车到蒸汽机车,再到内燃机车的演变过程。今天,我们已拥有汽车、火车、飞机等快速变通工具。
| 1. |
汽车、火车、飞机在行驶中都会因某些因素而影响其速度,所以高速运行的交通工具的头部一般呈流线型,主要是为了减少。 |
| 2. |
某汽车的部分参数如下表,请根据表中数据完成表的其他部分。
|
| 3. |
生活中经常用"呼啸而来"形容正在驶近的车辆,这是声波在传播过程中对接收者而言频率发生变化的表现,无线电波也具有这种效应。图中的测速雷达正在向一辆接近的车辆发生无线电波,并接收被车辆反射的无线电波。由于车辆的运动,接收的无线电波频率与发生时不同,利用频率差 就能计算出车辆的速度。已知发出和接收的频率间关系为,式中是真空中的光速,若,,可知被测车辆的速度大小为m/s。 |
| 4. |
有一个小实验:当向两片竖直放置的纸片的中间吹气时,会发现两个小纸片不但不分离,反而靠拢了。这一现象告诉我们,流体运动部分产生的压强要比它周围静止部分产生的压强小。也可以概括为流速大,压强小、流速小,压强大。飞机上天就是由于机翼上下空气流速不同造成的压力差所致。赛车在尾部都装有尾翼板,其作用是()
|
| 5. |
电动车所需能量由它所携带的蓄电池供给。右图为某类电动车与汽油车性能的比较。通常车用电动机的质量是汽油机的4倍或5倍。为促进电动车的推广使用,在技相主主要应对电动车的等部件加以改进。给电动车蓄电池充电的能量实际上来自于发电站。一般发电站燃烧燃料所释放出来的能量仅30%转化为电能,在向用户输送及充电过程中又损失了20%,这意味着使用电动车时能量转化的总数率约为%。
|
起重机竖直吊起一货物,货物的速度随时间的关系如图-3,物体上升运动有几个过程?每一阶段的加速度大小多少?6s内上升的高度是多少?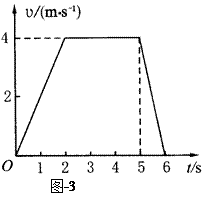
如图-2所示,某同学沿平直路面由A点出发前进了100 m到达斜坡底端的B点,又沿倾角为60°的斜面前进了100 m达到C点,求此同学的位移和路程。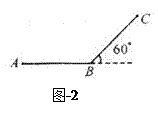
某运动员在百米跑道上以8 m/s的速度跑了80 m,然后又以2 m/s的速度走了20 m,这个运动员通过这段路的平均速度是多少?
如图表示做直线运动的质点从初位置A经过B运动到C,然后从C返回,运动到末位置B。设AB长7m , BC长5m , 求质点的位移的大小和路程。
在图中,汽车初位置的坐标是-2km,末位置的坐标是1km。求汽车的位移的大小和方向。