为了缩短下楼的时间,消防队员往往抱着竖直杆直接滑下,先以可能的最大加速度沿杆做匀加速直线运动,再以可能的最大加速度沿杆做匀减速直线运动.假设一名质量m="65" kg、训练有素的消防队员(可视为质点),在沿竖直杆无初速度滑至地面的过程中,重心共下移了s="11.4" m.已知该队员与杆之间的滑动摩擦力最大可达到fmax="975" N,队员着地的速度不能超过6 m/s.重力加速度g取10 m/s2,竖直杆表面各处的粗糙程度相同,且忽略空气对该队员的作用力.求:
(1)该队员下滑过程中动量的最大值;
(2)该队员下滑过程的最短时间.
下图代表不同细胞间的信息传递,1~8代表靶细胞的细胞结构,请根据图回答下列问题:
(1)图中的神经末梢和靶细胞C等共同构成________,若物质a是唾液淀粉酶,其合成、分泌过程依次经过的细胞器是________(填图中序号)。
(2)若刺激M点,则M点膜外电位变化是____________________,由此刺激引发的神经兴奋的传导方向与________(填“膜内”或“膜外”)的局部电流方向一致;若刺激N点,电流表将偏转________次。
(3)当兴奋抵达时,贮存在________内的神经递质释放出来,并与分布在突触后膜上的结构1________结合。突触间隙的神经递质可通过主动运输进入细胞再被利用。上述过程体现了细胞膜具有的功能是________________和________________。
(4)下列各项生命活动中,与细胞膜上的1无关的是________________
| A.K+ 进入小肠上皮细胞 | B.神经递质作用于突触后膜 |
| C.抗原致敏B淋巴细胞 | D.HIV侵染辅助性T淋巴细胞 |
下图甲表示某流速缓慢的河段,因A、B、C排污口不断排放氮、磷、有害物质a等污染物,使河段水体污染逐渐加重,1、2、3、4表示不同的调查段。图乙表示该河段中3号调查段各营养级的部分生物种类受污染的情况。请回答:
(1)受污河段中,若生态系统能够恢复稳态,恢复速度最快的是号调查段。随污染的加重,将造成下游的水体。
(2)图乙包含的食物链属于食物链,由于作用导致生物体内物质a含量沿食物链逐级增加。
(3)在4号调查段,若水生植食动物营养级中的浮游动物大量繁殖,造成数量剧增,此时水生植物和浮游动物之间可能会呈现上宽下窄的;若水生植食动物营养级中的鱼类出现大量死亡,将引发生态系统的
调节。
(4)对该河流进行治理,你认为可以采取的治理措施有、(写出2项)。
如图是某生态系统中的食物网结构模式图,下列相关叙述不正确的是()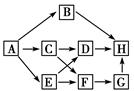
| A.在该食物网中,共有5条食物链存在 |
| B.在该食物网中,H处于三个不同的营养级 |
| C.在该食物网中,如果C种群的数量下降10%,则H的数量不会发生明显变化 |
| D.若B种群中各年龄期的个体数目比例适中,则该种群的密度在一段时间内会明显变大 |
下图是某雄性二倍体动物体内一个正在分裂的原始生殖细胞,图中字母表示其染色体上的部分基因。
请回答:
(1)该细胞正在进行_____________分裂,其直接产生的子细胞是_________________。
(2)这种基因型的动物可以形成哪4种比例相等的配子?___________。
(3)若要对该动物进行测交,则与其测交的个体应该有怎样的基因型?请在上方的圆圈中表示之。
有两个纯种小麦,一个是高秆抗锈病(DDTT),另一个是矮秆易染锈病(ddtt),现有实验三组:
第一组是: DDTT× ddtt → F1(自交)→ F2
第二组是: DDTT× ddtt → F1,并用F1的花粉培养得到单倍体
第三组是: DDTT进行X射线、紫外线综合处理。
实验结果发现:三组实验中都出现了矮秆抗锈病品种。试问:
(1)第一组F2出现矮秆抗锈病的几率是,在矮秆抗锈病中能稳定遗传的占。
(2)第二组使用的方法,在遗传育种上称为,其培育中首先要用的方法是花药离体培养;然后用使其染色体加倍,这种育种方法的优点是。
(3)第三组方法出现ddtt后代是偶然的、个别的,它是DDTT通过来实现的。