如图8-3-10,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上的O点,此时弹簧处于原长.另一质量与B相同的滑块A从导轨上的P点以初速度v0向B滑行,当A滑过距离l时,与B相碰.碰撞时间极短,碰后A、B粘在一起运动.设滑块A和B均可视为质点,与导轨的动摩擦因数均为μ.重力加速度为g.求: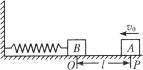
图8-3-10
(1)碰后瞬间,A、B共同的速度大小;
(2)若A、B压缩弹簧后恰能返回到O点并停止,求弹簧的最大压缩量.
蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目.一个质量为60 kg的运动员,从离水平网面3.2 m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0 m高处.已知运动员与网接触的时间为1.2 s,若把这段时间内网对运动员的作用力当作恒力处理,求此力的大小.(g取10 m/s2)
下面是一个物理演示实验,它显示:图2中自由下落的物体A和B经反弹后,B能上升到比初始位置高得多的地方.A是某种材料做成的实心球,质量m1="0.28" kg,在其顶部的凹坑中插着质量m2="0.10" kg的木棍B.B只是松松地插在凹坑中,其下端与坑底之间有小空隙.将此装置从A下端离地板的高度H="1.25" m处由静止释放.实验中,A触地后在极短的时间内反弹,且其速度大小不变;接着木棍B脱离A开始上升,而球A恰好停留在地板上.求木棍B上升的高度,重力加速度g取10 m/s2.
如图15所示,发射人造卫星时,先把卫星送入近地点Q,然后使其沿椭圆轨道到达远地点P,此时速度为v.若P点到地心的距离为R,卫星的总质量为m,地球半径为R0,地表的重力加速度为g,则欲使卫星从P点起绕地球做半径为R的圆轨道运动,卫星在P点处应将质量为Δm的燃气以多大的对地速度向后喷出?(将连续喷气等效为一次性喷气)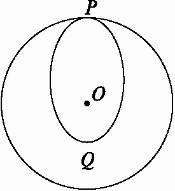
图15
如图14所示,在足够长的斜面上有一质量为m的长方形的木板A,木板表面光滑,当木板获得初速度v0后正好能沿斜面匀速下滑.当木板匀速下滑时将一质量也为m的滑块B轻放在木板表面上,当B在木板上滑动时,木板A和滑块B的加速度大小之比为多少?当B在木板上动量为3mv0/2时,木板的动量为多少?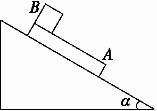
图14
平静的湖面上浮着一只长L="6" m、质量为550 kg的船,船头上站着一质量为m="50" kg的人,开始时,人和船均处于静止.若船行进时阻力很小,问当人从船头走到船尾时,船将行进多远?