设函数f(x)ax2bxc(a≠0)，曲线yf(x)通过点(-优题课

题文

设函数 $f (x) = a x^{2} + b x + c (a \neq 0)$ ，曲线 $y = f (x)$ 通过点 $(0, 2 a + 3)$ ，且在点 $(- 1, f (- 1))$ 处的切线垂直于 $y$ 轴.

（Ⅰ）用 $a$ 分别表示 $b$ 和 $c$ ；
（Ⅱ）当 $b c$ 取得最小值时，求函数 $g (x) = - f (x) e^{x}$ 的单调区间。

科目数学题型解答题难度中等

相关试题

(12分) 已知集合
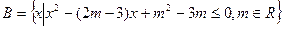
（1）若，求实数m的值；
（2）设全集为R，若，求实数m的取值范围。

(10分) 已知函数的定义域为，值域为[-5,4]．求a和b．

点A、B分别是椭圆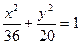长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于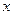轴上方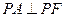，.求点P的坐标

已知抛物线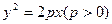的焦点为F，A是抛物线上横坐标为4、且位于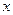轴上方的点，A到抛物线准线的距离等于5.过A作AB垂直于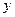轴，垂足为B，OB的中点为M.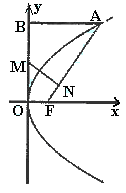

（1）求抛物线方程；
（2）过M作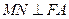，垂足为N，求点N的坐标；
（3）以M为圆心，MB为半径作圆M，当是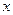轴上一动点时，讨论直线AK与圆M的位置关系.

双曲线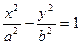(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥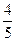c.求双曲线的离心率e的取值范围