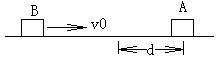如图所示，位于竖直平面内的坐标系xOy，在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场，磁感应强度大小为B，还有沿x轴负方向的匀强电场，场强大小为E．在其第一象限空间有沿y轴负方向的、场强为E/ =4/3E的匀强电场，并在y >h区域有磁感应强度也为B的垂直于纸面向里的匀强磁场．一个带电荷量为q的油滴从图中第三象限的P点得到一初速度，恰好能沿PO作直线运动（PO与x轴负方向的夹角为θ =37°），并从原点O进入第一象限．已知重力加速度为g，sin37°= 0.6，cos37°= 0.8，问：
(1)油滴的电性;
(2)油滴在P点得到的初速度大小;
(3) 油滴在第一象限运动的时间和离开第一象限处的坐标值．
1)请在图中画出通过A点的电场线？
2）该匀强电场强度的大小是多少？
3）一带电量为－4×10－6C的微粒沿AB运动，则电场力做正功还是负功，所做的功是多少？
4)电势能变化了多少？
5）若该微粒做匀速运动，则此微粒的质量为多少？
（cosθ=3/5,sinθ=4/5,取g＝10m／s2）
1)在离Q点10cm的A点的场强大小和方向?
2)若在A点放一电量为3.0×10-10C的负点电荷-q,则此负电荷受力大小和方向?
3)若此负电荷在A点静止释放,它将作什么性质的运动?(用一句话说出是加速还是减速,加速度大小是否变化,怎样变化,是直线还是曲线的运动)（k=9.0×109N.m2/C2)
如图是建筑工地常用的一种“深坑打夯机”，电动机带动两个滚轮匀速转动将夯杆从深坑提上来，当夯杆底端刚到达坑口时，两个滚轮彼此分开，将夯杆释放，夯杆在重力作用下落回深坑。夯实坑底。已知两个滚轮边缘的线速度恒为v=4m/s，滚轮对夯杆的压力FN=2×104N，滚轮与夯杆间的动摩擦因数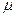
=0.3，夯杆质量m=1×103kg，坑深h=6.4m，取g=10m/s2，求：
（1）夯杆自坑底开始匀加速上升，当速度增加到4m/s时，夯杆上升的高度；
（2）夯杆自坑底上升的最大高度；
如图12所示，一个被x轴与曲线方程
（m）所围的空间中存在着匀强磁场。磁场方向垂直纸面向里，磁感应强度B=0.2T。正方形金属线框的边长是L=0.40m，电阻是R=0.1Ω，它的一边与x轴重合，在拉力F的作用下，线框以v=10m/s的速度水平向右匀速运动。试求：
（1）拉力F的最大功率是多少？
（2）拉力F要做多少功才能把线框拉过磁场区？
对于两物体碰撞前后在同一直线上，且无机械能损失的碰撞过程，可以简化为如下模型：A、B两物体位于光滑水平面上，仅限于沿同一直线运动。当它们之间的距离大于等于某一定值d时，相互作用力为零；当它们间的距离小于d时，存在大小恒为F的斥力。设A物体的质量m1=1.0kg，开始时静止在直线上某点；物体B质量为m2=3.0kg，以速度v0从远处沿直线向A运动，如图所示。若d=0.10m，F=0.60N，v0=0.20m/s，求：
（1）相互作用过程中A、B加速度大小；
（2）从发生相互作用到A、B间的距离最小，系统（物体组）动能的减小量