真空中存在空间范围足够大的、水平向右的匀强电场.在电场中,若将一个质量为m、带正电的小球由静止释放,运动中小球的速度与竖直方向夹角为37°(取sin37°=0.6,cos37°=0.8).现将该小球从电场中某点以初速度v0竖直向上抛出.求运动过程中: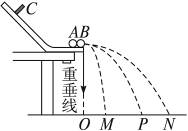
图16-2-5
(1)小球受到的电场力的大小及方向;
(2)小球从抛出点至最高点的电势能变化量;
(3)小球的最小动量的大小及方向.
A、B两辆汽车在一条东西方向的直路上向东行驶,若以地球为参考系,A速度为6m/s,B速度为10m/s。⑴若以A为参考系,B的速度多大?方向如何?⑵若以B为参考系, A的速度多大?方向如何?⑶以A或B为参考系,地面的运动情况如何?
敦煌曲子词中有一首:“满眼风光多闪烁,看山恰似走来迎,仔细看山山不动,是船行”.请用物理学知识解释“山走来”和“山不动,是船行”。你由此又得到什么看法?
⑴A车沿曲轨道刚滑到水平轨道时的速度v0;
⑵弹簧的弹性势能最大时A车的速度v和弹簧的弹性势能Ep
⑴碰撞结束时小球A的速度vA
⑵小球A与小球B碰撞前的速度v0的大小.
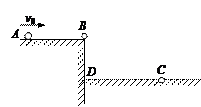
一打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下来,打出的纸带的一段如图所示。
为了求出小车在下滑过程中所受的阻力,还需要测量的物理量有哪些?用测得的量表示加速度a。