已知椭圆 的左、右焦点分别为
的左、右焦点分别为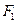 ,
,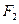 .过
.过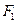 的直线交椭圆于
的直线交椭圆于 两点,过
两点,过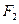 的直线交椭圆于
的直线交椭圆于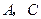 两点,且
两点,且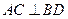 ,垂足为
,垂足为 .
.
(Ⅰ)设 点的坐标为
点的坐标为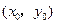 ,证明:
,证明: ;
;
(Ⅱ)求四边形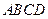 的面积的最小值.
的面积的最小值.
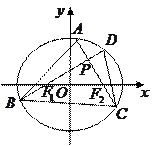 |
(本小题满分12分)
已知A、B两点的坐标分别是(-1,0)、(1,0),直线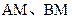 相交于点
相交于点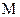 ,且它们的斜率之积为
,且它们的斜率之积为 ,求点
,求点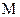 的轨迹方程并判断轨迹形状。
的轨迹方程并判断轨迹形状。
(本小题满分12分)
求适合下列条件的圆锥曲线方程:
(1).长轴长是短轴长的3倍,经过点(3,0)的椭圆标准方程。
(2).已知双曲线两个焦点的坐标为 ,双曲线上一点P到两焦点的距离之差的绝对值等于6,求双曲线标准方程.
,双曲线上一点P到两焦点的距离之差的绝对值等于6,求双曲线标准方程.
(3).已知抛物线的顶点在原点,准线与其平行线x=2的距离为3,求抛物线标准方程.
(本小题满分12分)
已知命题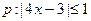 ,命题
,命题 ,若
,若 是
是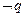 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
已知函数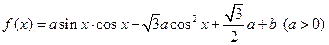
(1)写出函数的单调递减区间;
(2)设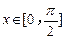 ,
, 的最小值是
的最小值是 ,最大值是
,最大值是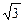 ,求实数
,求实数 的值.
的值.
已知△ABC的内角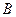 满足
满足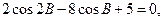 ,若
,若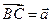 ,
,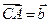 且
且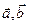 满足:
满足: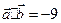 ,
,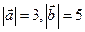 ,
,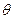 为
为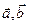 的夹角.求
的夹角.求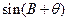 。
。