
(1)弹簧的原长.
(2)弹簧的倔强系数.
(3)弹簧伸长0.05m时,弹力的大小.
(1)小球运动到B点时的动能
(2)小球下滑到距水平轨道的高度为1/2R时的速度大小
(3)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力NB、NC各是多大?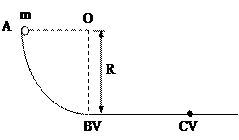
、在某些恒星内,3个α粒子结合成1个 核,
核, 原子的质量是12.0000u,
原子的质量是12.0000u,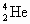 原子的质量是4.0026u.已知
原子的质量是4.0026u.已知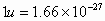 kg,则
kg,则
反应过程中的质量亏损是多少kg?反应过程中释放的能量是多少J?
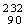 Th经过
Th经过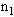 次
次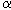 衰变,
衰变,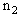 次
次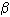 衰变后变为铅
衰变后变为铅 Pb.求
Pb.求
用质量为m的电子去轰击一个质量为M、最初静止的氢原子可以使其从基态跃迁到某激发态,设该激发态和基态的能量差为ΔE,欲使上述跃迁能够发生,电子的最小初动能是多大?