甲乙二人轮流掷一枚均匀的正方体骰子,规定:如果某人某一次掷出1点,则下一次继续由此人掷,如果掷出其他点数,则由另一人来掷,且第一次由甲掷.设第n次由甲掷的概率为pn,由乙掷的概率为qn.
(1)计算p2,p3的值;
(2)求证{pn-qn}是等比数列;
(3)求pn.
(本小题满分13分,(1)小问6分,(2)小分7分.)
进行一次掷骰子放球游戏,规定:若掷出1点,甲盒中放一球;若掷出2点或3点,乙
盒中放一球;若掷出4点或5点或6点,丙盒中放一球,共掷4次.
(1)求丙盒中至少放3个球的概率;
(2)记甲、乙两盒中所放球的总数为随机变量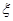 ,求
,求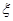 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)
设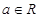 ,函数
,函数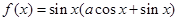 满足
满足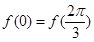 ,求
,求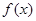 在
在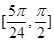 上的
上的
最大值和最小值.
.已知函数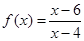
(1)求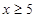 时
时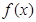 的取值范围;
的取值范围;
(2)若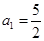 且
且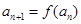 对任意
对任意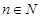 成立;
成立;
(ⅰ)求证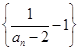 是等比数列;
是等比数列;
(ⅱ)令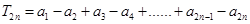 ,求证
,求证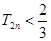 .
.
已知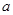 为实数,
为实数,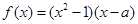
(Ⅰ)求导数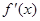 ;
;
(Ⅱ)若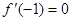 ,求
,求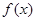 在
在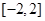 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)若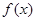 在
在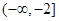 和
和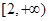 上都是递增的,求
上都是递增的,求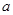 的取值范围.
的取值范围.
已知三棱锥 中,
中,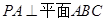 ,
,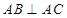 ,
,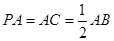 ,
, 为
为 上一点,
上一点,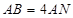 ,
, 分别为
分别为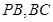 的中点.
的中点.
(1)证明: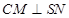 ;
;
(2)求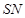 与平面
与平面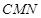 所成角的大小.
所成角的大小.