半径为a的圆形区域内有均匀磁场，磁感应强度为B="0.2" T,磁场方向垂直纸面向里，半径为b的金属圆环与磁场同心地放置，磁场与环面垂直，其中a="0.4" m,b="0.6" m.金属环上分别接有灯L1、L2，两灯的电阻均为R0="2" Ω，一金属棒MN与金属环接触良好，棒与环的电阻均忽略不计.
(1)若棒以v0="5" m/s的速率在环上向右匀速滑动，求棒滑过圆环直径OO′的瞬时(如图16-2-12所示)MN中的电动势和流过灯L1的电流.
图16-2-12
(2)撤去中间的金属棒MN，将右面的半圆环OL2O′以OO′为轴向上翻转90°，若此时磁场随时间均匀变化，其变化率为
T/s,求L1的功率.
如图所示，两根相距为d 的足够长的光滑金属导轨位于水平的xoy平面内，一端接有阻值为R的电阻。在x＞0的区域存在垂直纸面向里的磁场，磁感应强度B随x的增大而增大，B＝kx，式中k是一常量。一质量为m的金属杆地（地应为与）金属导轨垂直，可在导轨上滑动，当t＝0时位于x＝0处，速度为v0，方向沿x轴的正方向。在运动过程中，有一大小可调节方向始终不变的外力F作用于金属杆以保证金属杆的加速度恒定，大小为a，方向沿x轴的负方向。当金属杆的速度大小为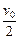
时，求所加外力F的大小。没（应为设）金属导轨与金属杆的电阻不计。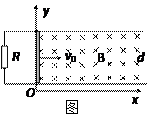
飞行时间质谱仪可通过测量离子飞行时间得到离子的荷质比
，如图1。带正电的离子经电压为U的电场加速后进入长度为L的真空管
，可测得离子飞越
所用时间
。改进以上方法，如图2，让离子飞越AB后进入场强为
（方向如图）的匀强电场区域
，在电场的作用下离子返回
端，此时，测得离子从
出发后飞行的总时间
，（不计离子重力）
⑴忽略离子源中离子的初速度，①用
计算荷质比；②用
计算荷质比。
⑵离子源中相同荷质比离子的初速度不尽相同，设两个荷质比都为
的离子在
端的速度分别为
和
，在改进后的方法中，它们飞行的总时间通常不同，存在时间差
，可通过调节电场
使
。求此时
的大小。
两块竖直放置的平行金属大平板A、B，相距d，两极间的电压为U，一带正电的质点从两板间的M点开始以竖直向上的初速度v0运动，当它到达电场中某点N点时，速度变为水平方向，大小仍为V0，如图所示．求M、N两点问的电势差．（忽略带电质点对金属板上电荷均匀分布的影响）
如图所示，一矩形绝缘木板放在光滑水平面上，另一质量为m、带电量为q的小物块沿木板上表面以某一初速度从A端沿水平方向滑入，木板周围空间存在足够大、方向竖直向下的匀强电场．已知物块与木板间有摩擦，物块沿木板运动到B端恰好相对静止．若将匀强电场的方向改为竖直向上，大小不变，且物块仍以原初速度沿木板上表面从A端滑入，结果物块运动到木板中点时相对静止．求：
⑴物块所带电荷的性质．
⑵匀强电场场强的大小
如图所示，由电源、定值电阻
和滑动变阻器
构成一闭合电路，一粒子加速枪并接在两端，在加速枪口
正上方
处的
点真空区域有一固定的点电荷，带电量为
。现有质量和带电量均不同的两种带负电静止粒子，从加速枪的左端加速后从点进入场区域，粒子射入枪口时速度方向垂直于
连线。
（1）试证明若加速电压
满足一定条件，两种粒子在场区域都能做匀速圆周运动。（不计粒子的重力）
（2）当滑动变阻器滑动头在某位置时，射出的带电粒子恰好做匀速圆周运动，若将
向左移动一小段距离后，该种粒子从加速枪中射出后的运轨迹变成什么形状？它的周期比圆周运动时长还是短？（只写明最后结论）