对于函数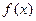 ,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=
,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=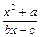 有且仅有两个不动点0和2.
有且仅有两个不动点0和2.
(Ⅰ)试求b、c满足的关系式;
(Ⅱ)若c=2时,各项不为零的数列{an}满足4Sn·f(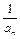 )=1,
)=1,
求证: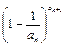 <
<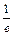 <
<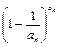 ;
;
(Ⅲ)设bn=-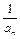 ,Tn为数列{bn}的前n项和,求证:T2009-1<ln2009<T2008.
,Tn为数列{bn}的前n项和,求证:T2009-1<ln2009<T2008.
已知抛物线的顶点为椭圆
 的中心,椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行.又抛物线与椭圆交于点
的中心,椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行.又抛物线与椭圆交于点 ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程.
已知棱长为 的正方体
的正方体 ,点
,点 、
、 分别是
分别是 和
和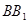 的中点,建立如图所示的空间直角坐标系.
的中点,建立如图所示的空间直角坐标系.
(1)写出图中 、
、 的坐标;
的坐标;
(2)求直线 与
与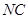 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)设椭圆C: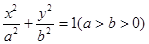 的左、右焦点分别为
的左、右焦点分别为 ,
, ,点
,点 满足
满足
(Ⅰ)求椭圆C的离心率 ;
;
(Ⅱ)若已知点 ,设直线
,设直线 与椭圆C相交于A,B两点,且
与椭圆C相交于A,B两点,且 ,
,
求椭圆C的方程。
(本小题满分12分)某地区为了了解中学生开展体育活动的情况,拟采用分层抽样的方法从A,B,C三市中抽取4所学校进行调查,已知A,B,C市中分别有26,13,13所学校.
(Ⅰ)求从A,B,C市中分别抽取的学校数;
(Ⅱ)若从抽取的4所学校中随机抽取2个进行调查结果的对比,计算这2所中至少有一个来自A市的概率.
(本小题满分12分)如图,在矩形ABCD中AB="1," BC= , 点P为矩形ABCD所
, 点P为矩形ABCD所
在平面外一点,PA⊥平面ABCD,点E为PA的中点。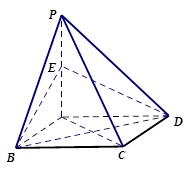
(Ⅰ)求证:PC//平面BED;
(Ⅱ)求直线BD与平面PAB所成的角的大小.