(本大题12分)如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线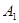 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .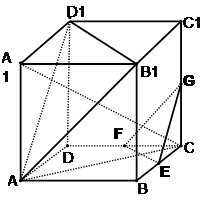
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=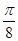 .
.
(1)求φ;
(2)求函数y=f(x)的单调增区间.
已知函数y=Asin(ωx+φ)(A>0、ω>0,|φ|<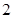 )的图象的一个最高点为(2,2
)的图象的一个最高点为(2,2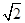 ),由这个最高点到相邻最低点,图象与x轴交于(6,0)点,试求这个函数的解析式.
),由这个最高点到相邻最低点,图象与x轴交于(6,0)点,试求这个函数的解析式.
如图为函数y=Asin(ωx+φ)的图象的一段.试确定函数y=Asin(ωx+φ)的解析式.
(本小题满分16分)已知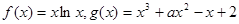
(I)如果函数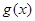 的单调递减区间为
的单调递减区间为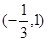 ,求函数
,求函数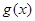 的解析式;
的解析式;
(II)在(Ⅰ)的条件下,求函数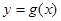 的图像在点
的图像在点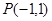 处的切线方程;
处的切线方程;
(III)若不等式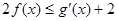 恒成立,求实数
恒成立,求实数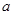 的取值范围.
的取值范围.
(本小题满分14分)在平面直角坐标系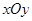 中,
中,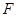 是抛物线
是抛物线
 的焦点,
的焦点,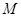 是抛物线
是抛物线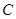 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过 三点的圆的圆心为
三点的圆的圆心为 ,点
,点 到抛物线
到抛物线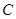 的准线的距离为
的准线的距离为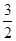 .(Ⅰ)求抛物线
.(Ⅰ)求抛物线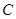 的方程;(Ⅱ)是否存在点
的方程;(Ⅱ)是否存在点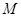 ,使得直线
,使得直线 与抛物线
与抛物线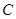 相切于点
相切于点 若存在,求出点
若存在,求出点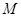 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.