（本小题满分12分）将一张2×6米的硬钢板按图纸的要求进行操作：沿线裁去阴影部分，把剩余的部分按要求焊接成一个有盖的长方体水箱（⑦为底，①②③④为侧面，⑤+⑥为水箱盖，其中①与③、②与④分别是全等的矩形，且⑤+⑥=⑦），设水箱的高为x米，容积为y立方米。
（1）写出y关于x的函数关系式；
（2）如何设计x的大小，使得水箱的容积最大？
已知半径为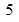
的圆的圆心在
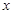轴上，圆心的横坐标是整数，且与
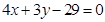相切．
（Ⅰ）求圆的方程；
（Ⅱ）设直线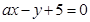
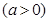与圆相交于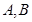
两点，求实数
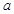的取值范围；
（Ⅲ）在（Ⅱ）的条件下，是否存在实数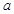，使得弦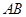
的垂直平分线
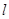过点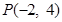
，若存在，求出实数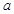的值；若不存在，请说明理由．
为了保护水资源，提倡节约用水，某市对居民生活用水收费标准如下：每户每月用水不超过6吨时每吨3元，当用水超过6吨但不超过15吨时，超过部分每吨5元，当用水超过15吨时，超过部分每吨10元。
（1）求水费y（元）关于用水量x（吨）之间的函数关系式；
（2）若某户居民某月所交水费为93元，试求此用户该月的用水量。
已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是 AB、PC的中点．
(1) 求证：EF∥平面PAD；
(2) 求证：EF⊥CD；
(3) 若∠PDA＝45°，求EF与平面ABCD所成的角的大小．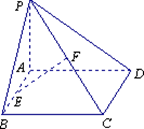
在正方体ABCD－A1B1C1D1中，E、F为棱AD、AB的中点．
（1）求证：EF∥平面CB1D1；
（2）求证：平面CAA1C1⊥平面CB1D1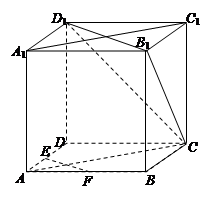
已知函数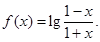
（1）求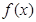
的定义域;（2）证明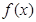函数是奇函数。