(本小题满分12分)
已知函数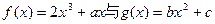 的图像都过点P(2,0),且在点P处
的图像都过点P(2,0),且在点P处
有相同的切线。
(I)求实数a、b、c的值;
(II)设函数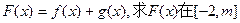 上的最小值。
上的最小值。
已知 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值;
(2)求展开式中系数最大的项.
设 为三角形
为三角形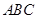 的三边,求证:
的三边,求证: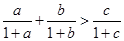
已知圆 的方程为
的方程为 ,直线
,直线
 ,设点
,设点 .
.
(1)若点 在圆
在圆 外,试判断直线
外,试判断直线 与圆
与圆 的位置关系;
的位置关系;
(2)若点 在圆
在圆 上,且
上,且 ,
, ,过点
,过点 作直线
作直线 分别交圆
分别交圆 于
于 两点,且直线
两点,且直线 和
和 的斜率互为相反数;
的斜率互为相反数;
① 若直线 过点
过点 ,求
,求 的值;
的值;
② 试问:不论直线 的斜率怎样变化,直线
的斜率怎样变化,直线 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.
设 是数列
是数列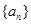 的前
的前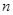 项和,且
项和,且 .
.
(1)当 ,
, 时,求
时,求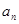 ;
;
(2)若数列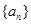 为等差数列,且
为等差数列,且 ,
, .
.
①求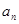 ;
;
②设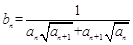 ,且数列
,且数列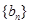 的前
的前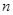 项和为
项和为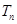 ,求
,求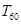 的值.
的值.
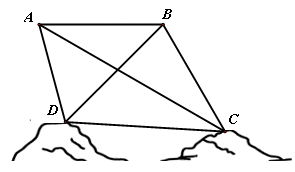
为绘制海底地貌图,测量海底两点 ,
, 间的距离,海底探测仪沿水平方向在
间的距离,海底探测仪沿水平方向在 ,
, 两点进行测量,
两点进行测量, ,
, ,
, ,
, 在同一个铅垂平面内. 海底探测仪测得
在同一个铅垂平面内. 海底探测仪测得


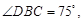
 ,
, 两点的距离为
两点的距离为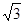 海里.
海里.
(1)求 的面积;
的面积;
(2)求 ,
, 之间的距离.
之间的距离.