(本小题满分13分)
若数列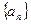
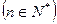 满足:(1)
满足:(1) ;(2)
;(2)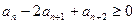 ;
;
(3) ,则称数列
,则称数列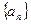 为“和谐”数列.
为“和谐”数列.
(Ⅰ)验证数列 ,其中
,其中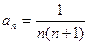 ,
,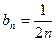 是否为“和谐”数列;
是否为“和谐”数列;
(Ⅱ)若数列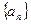 为“和谐”数列,证明:
为“和谐”数列,证明: .
.
函数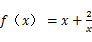 .
.
(1)判断 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)用函数单调性的定义证明函数 在
在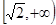 内是增函数.
内是增函数.
设全集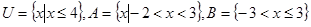 .
.
求(1)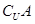 ;(2)
;(2)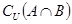 ;(3)
;(3) .
.
某班有学生55人,其中音乐爱好者34人,体育爱好者43人,还有4人既不爱好体育也不爱好音乐,则班级中既爱好体育又爱好音乐的有人.
已知函数 是定义域为
是定义域为 ,且
,且 同时满足以下条件:
同时满足以下条件:
① 在
在 上是单调函数;
上是单调函数;
②存在闭区间 (其中
(其中 ),使得当
),使得当 时,
时, 的取值集合也是
的取值集合也是 .则称函数
.则称函数
 是“合一函数”.
是“合一函数”.
(1)请你写出一个“合一函数”;
(2)若 是“合一函数”,求实数
是“合一函数”,求实数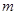 的取值范围.
的取值范围.
(注:本题求解中涉及的函数单调性不用证明,直接指出是增函数还是减函数即可)
已知 、
、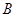 、
、 为函数
为函数 的图像上的三点,它们的横坐标分别是
的图像上的三点,它们的横坐标分别是 ,
, ,
, .
.
(1)设△ 的面积为
的面积为 ,求
,求 ;
;
(2)求函数 的值域.
的值域.