［物理——选修3－4］
（1）其振动系统的固有频率为f0，在周期性驱动力的作用下做受迫振动，驱动力的频率为f。若驱动力的振幅保持不变，下列说法正确的是 _____（填入选项前的字母，有填错的不得分）
| A．当f＜f0时，该振动系统的振幅随f增大而减小 |
| B．当f＞f0时，该振动系统的振幅随f减小而增大 |
| C．该振动系统的振动稳定后，振动的频率等于f0 |
| D．该振动系统的振动稳定后，振动的频率等于f |
（2）一棱镜的截面为直角三角形ABC，∠A＝30º，斜边AB＝a。棱镜材料的折射率为n＝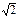
。在此截面所在的平面内，一条光线以45º的入射角从AC边的中点M射入棱镜。画出光路图，并求光线从棱镜射出的点的位置（不考虑光线沿原路返回的情况）。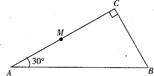
如图Ox、Oy、Oz为相互垂直的坐标轴，Oy轴为竖直方向，整个空间存在竖直向下的匀强磁场，磁感应强度大小为B．现有一质量为
、电量为q的小球从坐标原点O以速度v0沿Ox轴正方向抛出（不计空气阻力，重力加速度为g）．求：
（1）若在整个空间加一匀强电场E1，使小球在xOz平面内做匀速圆周运动，求场强E1和小球运动的轨道半径；
（2）若在整个空间加一匀强电场E2，使小球沿Ox轴做匀速直线运动，求E2的大小；
（3）若在整个空间加一沿y轴正方向的匀强电场，求该小球从坐标原点O抛出后，经过y轴时的坐标y和动能Ek；
一辆质量为m的汽车，以恒定的输出功率P在倾角为θ的斜坡上沿坡匀速行驶，如图所示，汽车受到的摩擦阻力恒为f（忽略空气阻力）.求：（1）汽车的牵引力F和速度v的表达式；（2）根据F与v的表达式，联系汽车上、下坡的实际，你能得到什么启发？
在水平长直的轨道上，有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动．某时刻将一质量为m的小滑块轻放到车面的中点，滑块与车面间的动摩擦因数为μ．
（1）证明：若滑块最终停在小车上，滑块和车摩擦产生的内能与动摩擦因数μ无关，是一个定值．
（2）已知滑块与车面间动摩擦因数μ=0.2，滑块质量m=1kg，车长L=2m，车速v0=4m/s，取g=10m/s2，当滑块放到车面中点的同时对该滑块施加一个与车运动方向相同的恒力F，要保证滑块不能从车的左端掉下，恒力F大小应该满足什么条件？
（3）在（2）的情况下，力F取最小值，要保证滑块不从车上掉下，力F的作用时间应该在什么范围内?
 |
如图(a)所示，两根足够长的光滑平行金属导轨相距为L，导轨平面与水平面成θ角，上端通过导线连接阻值为R的电阻，阻值为r的金属棒ab放在两导轨上，棒与导轨垂直并保持良好接触，整个装置处在垂直导轨平面向上的磁场中，若所加磁场的磁感应强度大小恒为B，使金属棒沿导轨由静止向下运动，金属棒运动的v-t图象如图（b）所示，当t=t0时刻，物体下滑距离为s。已知重力加速度为g,，导轨电阻忽略不计。试求：
（1）金属棒ab匀速运动时电流强度I的大小和方向；
（2）导体棒质量m；
（3）在t0时间内电阻R产生的焦耳热．
如图所示，第四象限内有互相正交的匀强电场E与匀强磁场B1， E的大小为0.5×103V/m, B1大小为0.5T；第一象限的某个矩形区域内，有方向垂直纸面向里的匀强磁场B2，磁场的下边界与x轴重合．一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动，经P点即进入处于第一象限内的磁场B2区域．一段时间后，小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为(0，-10)，N点的坐标为(0，30)，不计粒子重力，g取10m/s2．
(1)请分析判断匀强电场E1的方向并求出微粒的运动速度v；
(2)匀强磁场B2的大小为多大？；
(3) B2磁场区域的最小面积为多少？