(本小题满分13分)
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(I)若某位顾客消费128元,求返券金额不低于30元的概率;
(II)若某位顾客恰好消费280元,并按规则 参与了活动,他获得返券的金额记为X(元).
参与了活动,他获得返券的金额记为X(元).
求随机变量X的分布列和数学期望。
某工厂有214名工人, 现要生产1500件产品, 每件产品由3个A型零件与1个B型零件配套组成, 每个工人加工5个A型零件与3个B型零件所需时间相同. 现将全部工人分为两组, 分别加工一种零件, 同时开始加工. 设加工A型零件的工人有x人, 在单位时间内每人加工A型零件5k个(k∈N*), 加工完A型零件所需时间为g(x), 加工完B型零件所需时间为h (x).
(Ⅰ) 试比较 与
与 大小, 并写出完成总任务的时间
大小, 并写出完成总任务的时间 的表达式;
的表达式;
(Ⅱ) 怎样分组才能使完成任务所需时间最少?
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,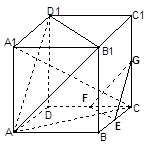
(1)求证:平面A B1D1∥平面EFG;
(2)求证:平面AA1C⊥面EFG.
(3)求异面直线AC与A1B所成的角
(本小题满分12分) 若函数 的图象过
的图象过 与
与 两点,设函数
两点,设函数 ;
;
(1)求 的定义域;
的定义域;
(2)求函数 的值域,判断g(x)奇偶性,并说明理由.
的值域,判断g(x)奇偶性,并说明理由.
(本小题满分12分)已知直线l经过点(0,-2),其倾斜角是60°.
(1)求直线l的方程;(2)求直线l与两坐标轴围成三角形的面积.
已知集合M={x|x2-3x+2=0},N={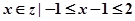 },Q={1,m2+1,m+1}
},Q={1,m2+1,m+1}
(1)求M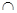 N;(2) 若M
N;(2) 若M Q,求实数m的值。
Q,求实数m的值。