已知函数
 ,函数
,函数 :
:
(1)当 时,求函数
时,求函数 的表达式;
的表达式;
(2)若 ,函数
,函数 在
在 上的最小值是2 ,求
上的最小值是2 ,求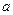 的值;
的值;
(3)在(2)的条件下,求直线 与函数
与函数 的图象所围成图形的面积.
的图象所围成图形的面积.
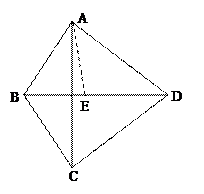
如图:在四面体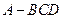 中,
中,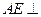 平面
平面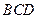 ,
,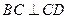 ,
,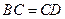 ,
,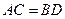 ,
,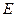 是
是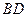 的中点;
的中点;
(1)求证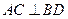 ;
;
(2)求直线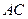 与平面
与平面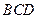 所成的角。
所成的角。
 |
设两个非零向量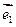 和
和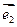 不共线;
不共线;
(1)试确定实数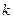 ,使
,使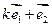 和
和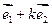 共线;
共线;
(2)若 ,
,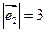 ,
,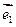 与
与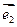 的夹角为60°,试确定
的夹角为60°,试确定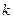 ,使
,使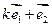 与
与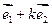 垂直。
垂直。
已知函数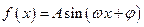
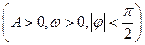 的部分图象如图所示
的部分图象如图所示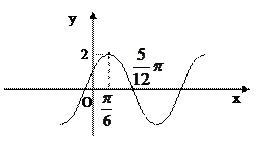 (1)求函数
(1)求函数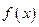 的解析式;
的解析式;
(2)如何由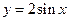 的图象通过
的图象通过
适当的变换得到函数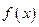 的
的
图象,写出变换过程。
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从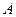 、
、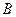 、
、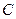 三个区中抽取7个工厂进行调查,已知
三个区中抽取7个工厂进行调查,已知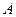 、
、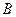 、
、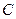 区中分别有18、27、18个工厂。
区中分别有18、27、18个工厂。
(1)求从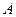 、
、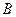 、
、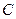 区中应分别抽取的工厂个数;
区中应分别抽取的工厂个数;
(2)若从抽得的7个工厂中随机抽取2个进行调查结果的对比,用列举法计算这2个工厂中至少有1个来自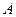 区的概率。
区的概率。
若对于一切实数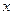 、
、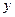 ,都有
,都有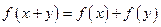
(1)求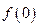 并证明
并证明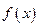 为奇函数;
为奇函数;
(2)若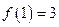 ,求
,求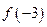 。
。