在△ABC中，内角A、B、C对边的边长分别是a、b、c.已知c=2,C=
.
（1）若△ABC的面积等于
，求a、b的值；
（2）若sinC+sin(B-A)=2sin2A,求△ABC的面积.
（本小题满分13分）
已知：定义在R上的函数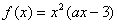
，其中a为常数。
（1）若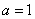
，求：
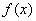的图象在点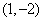
处的切线方程；
（2）若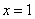
是函数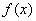的一个极值点，求：实数a的值；
（3）若函数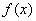在区间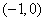
上是增函数，求：实数a的取值范围
（本小题满分13分）
已知：若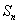
是公差不为0的等差数列
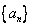的前
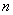项和，且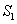
、
、
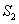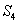成等比数列。
（1）求：数列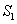、、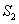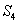的公比；
（2）若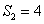
，求：数列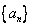的通项公式
（本小题满分13分）
已知：函数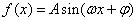
（其中
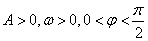）的图象与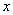
轴的交点中，相邻两个交点之间的距离为
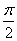，且图象上一个最低点为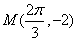
（1）求：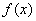
的解析式；
（2）当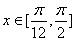
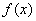，求：函数的值域
（本小题满分14分）
已知：函数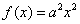
（
），
．
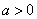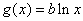（1）若函数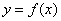
图象上的点到直线
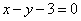距离的最小值为
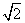，求
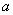的值；
（2）关于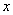
的不等式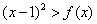
的解集中的整数恰有3个，求实数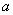的取值范围；
（3）对于函数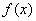
与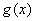
定义域上的任意实数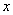，若存在常数
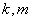，使得不等式
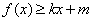和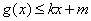
都成立，则称直线
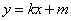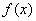为函数与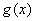的“分界线”。设
，
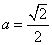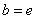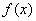，试探究与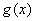是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
（本小题满分14分）
已知：函数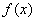
是定义在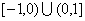
上的偶函数，当
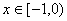时，
为实数）.
（1）当
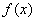时，求的解析式；
（2）若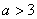
，试判断
上的单调性，并证明你的结论；
（3）是否存在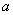
，使得当
有最大值1？若存在，求出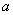的值;若不存在，请说明理由.