（本小题满分13分）
已知：函数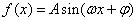
（其中
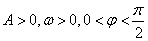）的图象与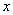
轴的交点中，相邻两个交点之间的距离为
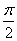，且图象上一个最低点为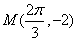
（1）求：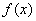
的解析式；
（2）当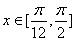
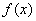，求：函数的值域
已知函数
⑴若
是该函数的一个极值点，求函数
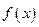的单调区间
⑵若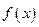在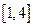
上是单调减函数，求
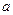的取值范围
用半径为6cm的圆形铁皮剪出一个圆心角为
的扇形，制成一个圆锥形容器，扇形的圆心角多大时，容器的容积最大．
已知曲线
与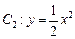
在第一象限内交点为
P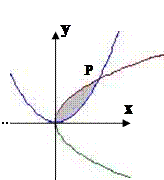
（1）求过点P且
与曲线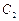
相切的直线方程；
（2）求两条曲线所围图形（如图所示阴影部分）的面积S.
设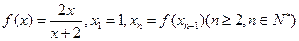
。
（1）求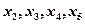
的值；
（2）归
纳{
}的通项公式，并用数学归纳法证明。
用红、黄、蓝、白、黑五种颜色在田字形的四个小方格内，每格涂一种颜色，相邻两格涂不同的颜色，如果颜色可以反复使用。
（1）从中任选四种颜色涂色，有多少种不同的涂法？
（2）按要求任意选色涂，共有多少种不同的涂法？