(本小题满分12分)已知函数 ,且当
,且当 时,
时, 的最小值为2,
的最小值为2,
(1)求 的值,并求
的值,并求 的单调递增区间;
的单调递增区间;
(2)先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的 ,再将所得的图象向右平移
,再将所得的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求方程
的图象,求方程 在区间
在区间 上所有根之和.
上所有根之和.
(本小题满分12分)设数列 的前n项和为
的前n项和为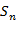 ,点
,点 均在函数y=x-2的图像上.
均在函数y=x-2的图像上.
(1)求数列 的通项公式;
的通项公式;
(2)求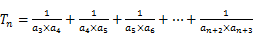 ;
;
(3)在(2)的条件下,求使得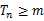 对所有
对所有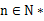 都成立的最大整数m.
都成立的最大整数m.
(本小题满分7分)选修4—5:不等式选讲
已知a+b=1,对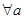 ,b∈(0,+∞),
,b∈(0,+∞), +
+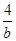 ≥|2x-1|-|x+1|恒成立,
≥|2x-1|-|x+1|恒成立,
(Ⅰ)求 +
+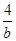 的最小值;
的最小值;
(Ⅱ)求x的取值范围。
选修4—4:坐标系与参数方程
已知曲线 的参数方程:
的参数方程:  (
( 为参数), 曲线
为参数), 曲线 上的点
上的点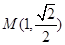 对应的参数
对应的参数 ,以坐标原点
,以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线 的极坐标方程;
的极坐标方程;
(Ⅱ)已知直线 过点P(1,0),且与曲线
过点P(1,0),且与曲线 于A,B两点,求
于A,B两点,求 的范围.
的范围.
(本小题满分7分)选修4—2:矩阵与变换
已知矩阵 ,试求曲线
,试求曲线 在矩阵
在矩阵 变换下的函数解析式.
变换下的函数解析式.