(本小题满分12分)已知函数 ,且当
,且当 时,
时, 的最小值为2,
的最小值为2,
(1)求 的值,并求
的值,并求 的单调递增区间;
的单调递增区间;
(2)先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的 ,再将所得的图象向右平移
,再将所得的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求方程
的图象,求方程 在区间
在区间 上所有根之和.
上所有根之和.
已知不等式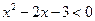 的解集为A,不等式
的解集为A,不等式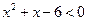 的解集为B。
的解集为B。
(1)求A∩B;
(2)若不等式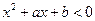 的解集为A∩B,求不等式
的解集为A∩B,求不等式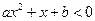 的解集。
的解集。
已知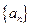 是等差数列,其中
是等差数列,其中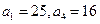
(1)求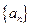 的通项;
的通项;
(2)数列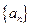 从哪一项开始小于0;
从哪一项开始小于0;
(3)求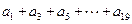 值。
值。
甲、乙两名跳高运动员一次试跳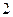 米高度成功的概率分别是
米高度成功的概率分别是 ,
, ,且每次试跳成功与否相互之间没有影响,求:
,且每次试跳成功与否相互之间没有影响,求:
(Ⅰ)甲试跳三次,第三次才成功的概率;
(Ⅱ)甲、乙两人在第一次试跳中至少有一人成功的概率;
(Ⅲ)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率.
在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.
(Ⅰ)求笼内恰好剩下1只果蝇的概率;
(Ⅱ)求笼内至少剩下5只果蝇的概率.
在医学生物学试验中,经常以果蝇作为试验对象,一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以ξ表示笼内还剩下的果蝇的只数.
(Ⅰ)写出ξ的分布列(不要求写出计算过程);
(Ⅱ)求数学期望Eξ;
(Ⅲ)求概率P(ξ≥Eξ).