设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6,0.5,0.5,0.4,各人是否使用设备相互独立,
(1)求同一工作日至少3人需使用设备的概率;
(2)实验室计划购买台设备供甲、乙、丙、丁使用,若要求"同一工作日需使用设备的人数大于的概率小于0.1,求的最小值.
已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的左、右焦点分别是
的左、右焦点分别是 的左、右顶点,而
的左、右顶点,而 的
的
左、右顶点分别是 的左、右焦点.
的左、右焦点.
(1)求双曲线 的方程;
的方程;
(2)若直线 与双曲线
与双曲线 恒有两个不同的交点A和B,且
恒有两个不同的交点A和B,且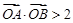 (其中
(其中 为原点),求实数
为原点),求实数 的范围.
的范围.
如图,正三棱柱(底面为正三角形,侧棱垂直于底面) 中,
中, 是
是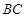 的中点,
的中点, 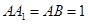 .
.
(1) 求证: ∥平面
∥平面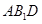 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
已知数列 与
与 ,若
,若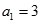 且对任意正整数
且对任意正整数 满足
满足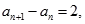 数列
数列 的前
的前 项和
项和 .(1)求数列
.(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前
的前 项和
项和
年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
| 健康指数 |
2 |
1 |
0 |
-1 |
| 60岁至79岁的人数 |
120 |
133 |
34 |
13 |
| 80岁及以上的人数 |
9 |
18 |
14 |
9 |
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”.
(1)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?
(2)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
在直角坐标系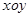 中,圆
中,圆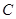 的参数方程
的参数方程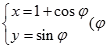 为参数).以
为参数).以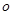 为极点,
为极点, 轴的非负半轴为极轴建
轴的非负半轴为极轴建
立极坐标系.
(1)求圆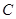 的极坐标方程;
的极坐标方程;
(2)直线 的极坐标方程是
的极坐标方程是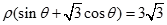 ,射线
,射线 与圆C的交点为
与圆C的交点为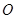 、
、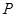 ,与直线
,与直线 的交点为
的交点为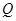 ,求线段
,求线段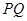 的长.
的长.