(1)某组同学设计了“探究加速度 与物体所受合力
与物体所受合力 及质量
及质量 的关系”实验.图(
的关系”实验.图( )为实验装置简图,A为小车,B为电火花计时器,C为装有细砂的小桶,D为一端带有定滑轮的长方形木板,实验中认为细绳对小车拉力
)为实验装置简图,A为小车,B为电火花计时器,C为装有细砂的小桶,D为一端带有定滑轮的长方形木板,实验中认为细绳对小车拉力 等于细砂和小桶的总重量,小车运动的加速度
等于细砂和小桶的总重量,小车运动的加速度 可用纸带上打出的点求得.
可用纸带上打出的点求得.
①图(b)为某次实验得到的纸带,已知实验所用电源的频率为50Hz.根据纸带可求出小车的加速度大小为 m/s2.(结果保留二位有效数字)
②在“探究加速度 与质量
与质量 的关系”时,保持细砂和小桶质量不变,改变小车质量
的关系”时,保持细砂和小桶质量不变,改变小车质量 ,分别记录小车加速度
,分别记录小车加速度 与其质量
与其质量 的数据.在分析处理数据时,该组同学产生分歧:甲同学认为应该根据实验中测得的数据作出小车加速度
的数据.在分析处理数据时,该组同学产生分歧:甲同学认为应该根据实验中测得的数据作出小车加速度 与其质量
与其质量 的图象.乙同学认为应该根据实验中测得的数据作出小车加速度
的图象.乙同学认为应该根据实验中测得的数据作出小车加速度 与其质量倒数
与其质量倒数 的图象.两位同学都按照自己的方案将实验数据在坐标系中进行了标注,但尚未完成图象(如下图所示).你认为同学 (填“甲”、“乙”)的方案更合理.请继续帮助该同学作出坐标系中的图象.
的图象.两位同学都按照自己的方案将实验数据在坐标系中进行了标注,但尚未完成图象(如下图所示).你认为同学 (填“甲”、“乙”)的方案更合理.请继续帮助该同学作出坐标系中的图象.
③在“探究加速度 与合力
与合力 的关系”时,保持小车的质量不变,改变小桶中细砂的质量,该同学根据实验数据作出了加速度
的关系”时,保持小车的质量不变,改变小桶中细砂的质量,该同学根据实验数据作出了加速度 与合力
与合力 的图线如图(
的图线如图( ),该图线不通过坐标原点,试分析图线不通过坐标原点的原因.
),该图线不通过坐标原点,试分析图线不通过坐标原点的原因.
答: .
(2)某待测电阻的额定电压为3V(阻值大约为10Ω).为测量其阻值,实验室提供了下列可选用的器材
A:电流表A1(量程300mA,内阻约1Ω)
B:电流表A2(量程0.6A,内阻约0.3Ω)
C:电压表V1(量程3.0V,内阻约3kΩ)
D:电压表V2(量程5.0V,内阻约5kΩ)
E:滑动变阻器R1(最大阻值为50Ω)
F:滑动变阻器R2(最大阻值为500Ω)
G:电源E(电动势4V,内阻可忽略)
H:电键、导线若干.
①为了尽可能提高测量准确度,应选择的器材为(只需填写器材前面的字母即可)
电流表_________;电压表___________;滑动变阻器_____________.
②下列给出的测量电路中,最合理的电路是
如图所示,车厢的质量为M,长度为L,静止在光滑水平面上。质量为m的木块(可看成质点)以速度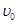 无摩擦地在车厢底板上向右运动,木块与车前壁碰撞后以
无摩擦地在车厢底板上向右运动,木块与车前壁碰撞后以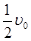 的速度向左运动,则再经过多长时间,木块将与车后壁相碰?
的速度向左运动,则再经过多长时间,木块将与车后壁相碰?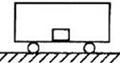
一列简谐横波沿x轴正方向传播,周期为T=2s,t=0时刻的波形如图所示。此刻,波刚好传到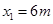 处,求:坐标
处,求:坐标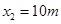 处的质点,经多长时间第一次经过平衡位置向y轴负方向运动?
处的质点,经多长时间第一次经过平衡位置向y轴负方向运动?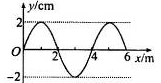
如图所示,用轻质活塞在气缸内封闭一定质量的理想气体,活塞与气缸壁之间的摩擦忽略不计。开始时活塞距气缸底的高度为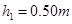 ,气体温度为
,气体温度为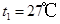 。给气缸加热,活塞缓慢上升到距气缸底的高度为
。给气缸加热,活塞缓慢上升到距气缸底的高度为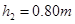 处时,缸内气体吸收Q=450J的热量。已知活塞横截面积
处时,缸内气体吸收Q=450J的热量。已知活塞横截面积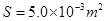 ,大气压强
,大气压强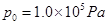 。求:
。求: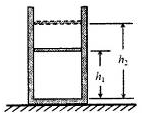
①加热后缸内气体的温度。
②此过程中缸内气体增加的内能 。
。
某放置在真空中的装置如图甲所示,水平放置的平行金属板A、B中间开有小孔,小孔的连线与竖直放置的平行金属板C、D的中心线重合。在C、D的下方有如图所示的、范围足够大的匀强磁场,磁场的理想上边界与金属板C、D下端重合,其磁感应强度随时间变化的图象如图乙所示,图乙中的 为已知,但其变化周期
为已知,但其变化周期 未知。已知金属板A、B之间的电势差为
未知。已知金属板A、B之间的电势差为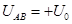 ,金属板C、D的长度均为L,间距为
,金属板C、D的长度均为L,间距为 。质量为m、电荷量为q的带正电粒子P(初速度不计、重力不计)进入A、B两板之间被加速后,再进入C、D两板之间被偏转,恰能从D极下边缘射出。忽略偏转电场的边界效应。
。质量为m、电荷量为q的带正电粒子P(初速度不计、重力不计)进入A、B两板之间被加速后,再进入C、D两板之间被偏转,恰能从D极下边缘射出。忽略偏转电场的边界效应。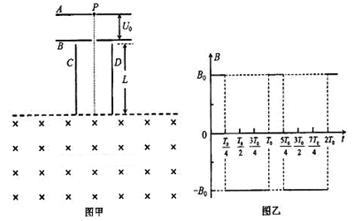
(1)求金属板C、D之间的电势差UCD。
(2)求粒子离开偏转电场时速度的大小和方向。
(3)规定垂直纸面向里的磁场方向为正方向,在图乙中t=0时刻该粒子进入磁场,并在 时刻粒子的速度方向恰好水平,求磁场的变化周期T0和该粒子从射入磁场到离开磁场的总时间t总。
时刻粒子的速度方向恰好水平,求磁场的变化周期T0和该粒子从射入磁场到离开磁场的总时间t总。
如图所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰好与两个固定在地面上的压力传感器X、Y相接触。图中AB高H=0.3m,AD长L=0.5m。斜面倾角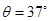 。可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数
。可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数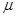 可以通过更换斜面表面的材料进行调节,调节范围是
可以通过更换斜面表面的材料进行调节,调节范围是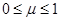 。
。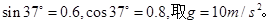

(1)令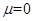 ,将P由D点静止释放,求P在斜面上的运动时间。
,将P由D点静止释放,求P在斜面上的运动时间。
(2)令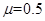 ,在A点给P一个沿斜面上的初速度
,在A点给P一个沿斜面上的初速度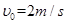 ,求P落地时的动能。
,求P落地时的动能。
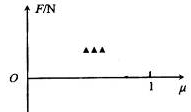
(3)将压力传感器X、Y接到同一个数据处理器上,已知当X和Y受到物块压力时,分别显示正值和负值。对于不同的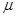 ,每次都在D点给P一个方向沿斜面向下、大小足够大的初速度,以保证它能滑离斜面。求滑行过程中处理器显示的压力F随
,每次都在D点给P一个方向沿斜面向下、大小足够大的初速度,以保证它能滑离斜面。求滑行过程中处理器显示的压力F随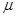 变化的函数关系式,并在坐标系中画出其函数图象。
变化的函数关系式,并在坐标系中画出其函数图象。