如图所示,可视为质点的物块A、B、C放在倾角为37O、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5,A与B紧靠在一起,C紧靠在固定挡板上,物块的质量分别为mA=0.80kg、mB=0. 40kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5C、qC=+2.0×10-5C,且保持不变。开始时三个物块均能保持静止且与斜面间均无摩擦力作用。如果选定两点电荷在相距无穷远处的电势能为0,则相距为r时,两点电荷具有的电势能可表示为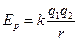 。现给A施加一平行于斜面向上的力F,使A在斜面上作加速度大小为a=2.5m/s2的匀加速直线运动,经过时间t0物体A、B分离并且力F变为恒力。当A运动到斜面顶端时撤去力F。
。现给A施加一平行于斜面向上的力F,使A在斜面上作加速度大小为a=2.5m/s2的匀加速直线运动,经过时间t0物体A、B分离并且力F变为恒力。当A运动到斜面顶端时撤去力F。
已知静电力常量k=9.0×109N·m2/C2,g=10m/s2,sin37O =0.6,cos37O =0.8。求:
(1)未施加力F时物块B、C间的距离;
(2)t0时间内库仑力做的功;
(3)力F对A物块做的总功。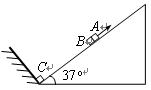
三只灯泡L1、L2和L3的额定电压分别为1.5 V、1.5 V和2.5 V,它们的额定电流都为0.3 A.若将它们连接成图1、图2所示电路,且灯泡都正常发光,
(1)试求图1电路的总电流和电阻R2消耗的电功率;
(2)分别计算两电路电源提供的电功率,并说明哪个电路更节能。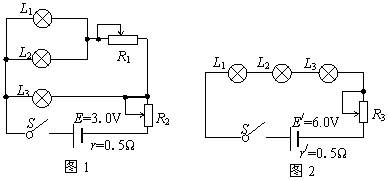
如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d="40" cm。电源电动势E=24V,内电阻r="1" Ω,电阻R="15" Ω。闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0="4" m/s竖直向上射入板间。若小球带电量为q=1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力。那么,滑动变阻器接入电路的阻值为多大时,小球恰能到达A板?此时,电源的输出功率是多大?(取g="10" m/s2)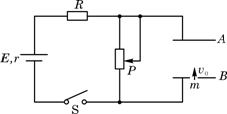
如图所示,在坐标系Oxy的第一象限中存在沿y轴正方向的匀速磁场,场强大小为E。在其它象限中存在匀强磁场,磁场方向垂直于纸面向里。A是y轴上的一点,它到坐标原点O的距离为h;C是x轴上的一点,到O的距离为L。一质量为m,电荷量为q的带负电的粒子以某一初速度沿x轴方向从A点进入电场区域,继而通过C点进入磁场区域。并再次通过A点,此时速度方向与y轴正方向成锐角。不计重力作用。试求:
⑴粒子经过C点速度的大小和方向;
⑵磁感应强度的大小B。
下图是导轨式电磁炮实验装置示意图。两根平行长直金属导轨沿水平方向固
定,其间安放金属滑块(即实验用弹丸)。滑块可沿导轨无摩擦滑行,且始终与导轨保持良好接触。电源提供的强大电流从一根导轨流入,经过滑块,再从另一导轨流回电源。滑块被导轨中的电流形成的磁场推动而发射。在发射过程中,该磁场在滑块所在位置始终可以简化为匀强磁场,方向垂直于纸面,其强度与电流的关系为B=kI,比例常量k=2.5×10-6T/A。
已知两导轨内侧间距l=1.5cm,滑块的质量m=30g,滑块沿导轨滑行5m后获得的发射速度v=3.0km/s(此过程视为匀加速运动)。
(1)求发射过程中电源提供的电流强度。
(2)若电源输出的能量有4%转换为滑块的动能,则发射过程中电源的输出功率和输出电压各是多大?
(3)若此滑块射出后随即以速度v沿水平方向击中放在水平面上的砂箱,它嵌入砂箱的深度为s'。设砂箱质量为M,滑块质量为m,不计砂箱与水平面之间的摩擦。求滑块对砂箱平均冲击力的表达式。
某植物园的建筑屋顶有太阳能发电系统,用来满足园内用电需要。已知该发电系统的输出功率为1.0×105W,输出电压为220V。求:
①按平均每天太阳照射6小时计,该发电系统一年(365天计)能输出多少电能?
②该太阳能发电系统除了向10台1000W的动力系统正常供电外,还可以同时供园内多少盏功率为100W,额定电压为220V的照明灯正常工作?
③由于发电系统故障,输出电压降为110V,此时每盏功率为100W、额定电压为220V的照明灯消耗的功率等是其正常工作时的多少倍?