(本小题满分16分)已知函数
(1)若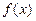 是区间(0,1)上单调函数,求
是区间(0,1)上单调函数,求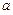 的取值范围;
的取值范围;
(2)若 ,试求
,试求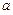 的取值范围。
的取值范围。
(满分12分)分已知函数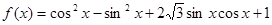 .
.
(1)求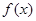 的最小正周期及
的最小正周期及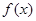 的最小值;
的最小值;
(2)若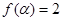 ,且
,且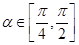 ,求
,求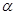 的值.
的值.
若二次项系数为a的二次函数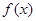 同时满足如下三个条件,求
同时满足如下三个条件,求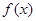 的解析式.
的解析式.
①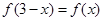 ;②
;②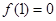 ;③对任意实数
;③对任意实数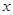 ,都有
,都有 恒成立.
恒成立.
(文) 设二次函数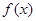 满足:(1)
满足:(1)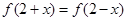 ,(2)被
,(2)被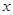 轴截得的弦长为2,(3)在
轴截得的弦长为2,(3)在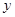 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式
(本小题满分12分)
过点Q 作圆C:
作圆C: 的切线,切点为D,且QD=4
的切线,切点为D,且QD=4
(1)求 的值
的值
(2)设P是圆C上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设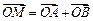 ,求
,求 的最小值(O为坐标原点)
的最小值(O为坐标原点)
已知:以点C (t, )(t∈R , t≠ 0)为圆心的圆与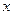 轴交于点O, A,与y轴交于点O, B,其中O为原点
轴交于点O, A,与y轴交于点O, B,其中O为原点
(1)求△OAB的面积的值
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程
(本小题满分12分)
已知一圆C的圆心为(2,-1),且该圆被直线 :x-y-1="0" 截得的弦长为2
:x-y-1="0" 截得的弦长为2 ,
,
(1)求该圆的方程
(2)求过弦的两端点的切线方程
(本小题满分12分)