如图,椭圆 的一个焦点为 ,且过点 .
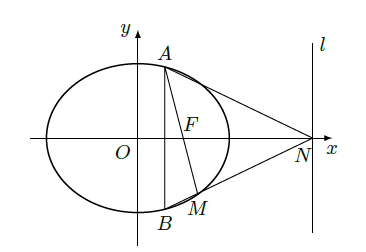
(Ⅰ)求椭圆
的方程;
(Ⅱ)若
为垂直于
轴的动弦,直线
与
轴交于点
,直线
与
交于点
.
(ⅰ)求证:点
恒在椭圆
上;(ⅱ)求
面积的最大值.
已知函数 ,
,
(1)当 且
且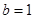 时,证明:对
时,证明:对 ,
, ;
;
(2)若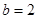 ,且
,且 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(3)数列 ,若存在常数
,若存在常数 ,
, ,都有
,都有 ,则称数列
,则称数列 有上界。已知
有上界。已知 ,试判断数列
,试判断数列 是否有上界.
是否有上界.
如图,已知抛物线 的焦点在抛物线
的焦点在抛物线 上.
上.
(1)求抛物线 的方程及其准线方程;
的方程及其准线方程;
(2)过抛物线 上的动点
上的动点 作抛物线
作抛物线 的两条切线
的两条切线 、
、 , 切点为
, 切点为 、
、 .若
.若 、
、 的斜率乘积为
的斜率乘积为 ,且
,且 ,求
,求 的取值范围.
的取值范围.
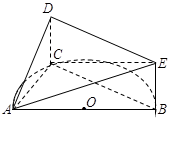
如图, 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 上除
上除 、
、 外的一个动点,
外的一个动点, 平面
平面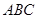 ,
, ,
, ,
, ,
, .
.
⑴证明:平面 平面
平面 ;
;
⑵试探究当 在什么位置时三棱锥
在什么位置时三棱锥 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值.
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车互不影响.假设李生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班,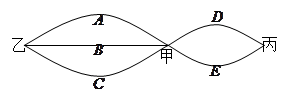
(1)写出李生可能走的所有路线;(比如DDA表示走D路从甲到丙,再走D路回到甲,然后走A路到达乙);
(2)假设从丙地到甲地时若选择走道路D会遇到拥堵,并且从甲地到乙地时若选择走道路B也会遇到拥堵,其它方向均通畅,但李生不知道相关信息,那么从出发到回到上班地没有遇到过拥堵的概率是多少?
已知点(1,2)是函数 的图像上一点,数列
的图像上一点,数列 的前n项和
的前n项和 .
.
(1)求数列 的通项公式;
的通项公式;
(2)将数列 前30项中的第3项,第6项,…,第3k项删去,求数列
前30项中的第3项,第6项,…,第3k项删去,求数列 前30项中剩余项的和.
前30项中剩余项的和.