设 函数
函数 是增函数,
是增函数, 函数
函数 在R上有极值,求使命题“p且q”为真的实数m的取值范围。
在R上有极值,求使命题“p且q”为真的实数m的取值范围。
有5张大小相同的卡片分别写着数字1、2、3、4、5,甲,乙二人依次从中各抽取一张卡片(不放回),试求:
(1)甲抽到写有奇数数字卡片,且乙抽到写有偶数数字卡片的概率;
(2)甲、乙二人至少抽到一张偶数数字卡片的概率。
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,如图所示茎叶图,根据茎叶图问:
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在 间的频率是多少?
间的频率是多少?
(3)甲、乙两个网站哪个更受欢迎?并说明理由。
设计一个算法,求表达式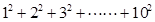 的值,并画出程序框图。
的值,并画出程序框图。
某公园内有一椭圆形景观水池,经测量知,椭圆长轴长为20米,短轴长为16米,现以椭圆长轴所在直线为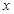 轴,短轴所在直线为
轴,短轴所在直线为 轴,建立平面直角坐标系,如图所示:
轴,建立平面直角坐标系,如图所示: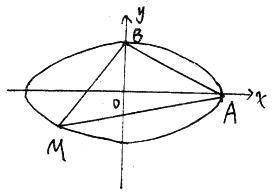
(1)为增加景观效果,拟在水池内选定两点安装水雾喷射口,要求椭圆上各点到这两点距离之和都相等,请指出水雾喷射口的位置(用坐标表示),并求椭圆的方程。
(2)为了增加水池的观赏性,拟划出一个以椭圆的长轴顶点A、短轴顶点B及椭圆上某点M构成的三角形区域进行夜景灯光布置,请确定点M的位置,使此三角形区域面积最大。