已知函数
,其中
,
为常数.
(1)当
时,求函数
的极值;
(2)当
时,证明:对任意的正整数
,当
时,有
.
设函数f(x)= (x>0且x≠1).
(x>0且x≠1).
(1)求函数f(x)的单调区间;
(2)已知2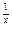 >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围.
已知函数f(x)=x3-ax2-3x.
(1)若f(x)在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=-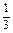 是f(x)的极值点,求f(x)在[1,a]上的最大值;
是f(x)的极值点,求f(x)在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
已知函数f(x)=x3-ax-1.
(1)若f(x)在实数集R上单调递增,求实数a的取值范围;
(2)是否存在实数a,使f(x)在(-1,1)上单调递减?若存在,求出a的取值范围;若不存在,说明理由;
(3)证明:f(x)=x3-ax-1的图象不可能总在直线y=a的上方.
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件.
(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a).