如图所示,空间存在垂直纸面向里的两个匀强磁场区域,磁感应强度大小均为B,磁场Ⅰ宽为L,两磁场间的无场区域为Ⅱ,宽也为L,磁场Ⅲ宽度足够大。区域中两条平行直光滑金属导轨间距为l,不计导轨电阻,两导体棒ab、cd的质量均为m,电阻均为r。ab棒静止在磁场Ⅰ中的左边界处,cd棒静止在磁场Ⅲ中的左边界处,对ab棒施加一个瞬时冲量,ab棒以速度v1开始向右运动。
(1)求ab棒开始运动时的加速度大小;
(2)ab棒在区域Ⅰ运动过程中,cd棒获得的最大速度为v2,求ab棒通过区域Ⅱ的时间;
(3)若ab棒在尚未离开区域Ⅱ之前,cd棒已停止运动,求:ab棒在区域Ⅱ运动过程中产生的焦耳热。
质量为5×10-6kg的带电粒子以2m/s速度从水平放置的平行金属板A、B中央沿水平方向飞入板间,如图所示.已知板长L=10cm,间距d=2cm,当UAB为1000V时,带电粒子恰好沿直线穿过板间,求该粒子带什么电?电量为多少?
在空间的部分区域中有一水平方向的匀强磁场,磁场的边界如图中的虚线所示。有一矩形线框abcd可以绕竖直的转动轴OOˊ匀角速转动,OOˊ恰好与磁场边界重合。在初始时刻,线框平面与磁场方向平行。已知磁场的磁感强度为B,线框ab边的长度为l,bc边的长度为2l,整个线框的电阻为R,线框转动的角速
度为ω,试求:
(1)线框位于图示位置时,线框中的感应电动势为多大?
(2)线框由图示位置转过30°时,线框受到的安培力矩为多大?
两根相距L=20cm的平行导轨,固定在绝缘板上,倾斜部分与水平方向成α=300角。在导轨的倾斜部分和水平部分分别放两根质量均为m=20g的铜棒,棒与导轨间的动摩擦因数μ=0.25,整个装置放在磁感强度B=0.1T竖直向上的匀强磁场中,如图所示,两根铜棒的总电阻R="0.2Ω," 导轨的电阻不计,求:
(1)cd棒开始运动时的电流多大?
(2)ab棒由斜面顶端静止下滑的速度达到多大时,静止在水平轨道上的cd棒才开始运动?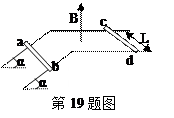
半径为r的光滑圆环固定在竖直平面内,竖直向下的匀强电场强度为E,与圆环所在平面垂直的匀强磁场的磁感强度为B。一质量为m,带正电量为q的球套在光滑圆环上,从A点由静止开始运动,求小球到达最低位置C(∠AOC=900)时:
(1)小球的速率;
(2)小球对圆环压力的大小。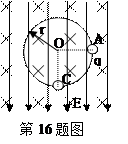
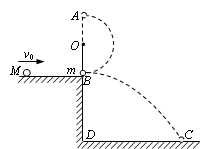
如图所示,O为一水平轴。细绳上端固定于O轴,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为 =0.6m。平台高BD=0.80m。一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳的约束下做圆周运动,经最高点A时,绳上的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2m。求:质量为M的小球与摆球碰撞前的速度大小(不计空气阻力,取g=10m/s2)。
=0.6m。平台高BD=0.80m。一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳的约束下做圆周运动,经最高点A时,绳上的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2m。求:质量为M的小球与摆球碰撞前的速度大小(不计空气阻力,取g=10m/s2)。