已知函数f(x)=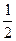 x
x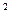 -ax+(a-1)
-ax+(a-1)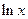 ,
,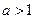 .讨论函数
.讨论函数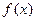 的单调性.
的单调性.
(本小题满分12分)解不等式: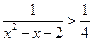
设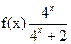 ,若
,若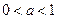 ,试求:
,试求:
(1)求 的值;
的值;
(2)求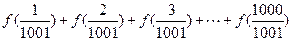 的值.
的值.
已知函数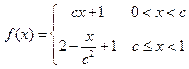 满足
满足
(1)求常数c的值;
(2)解不等式 .
.
光线通过一块玻璃,其强度要损失10%,把几块这样的玻璃重叠起来,设光线原来的强度为k,通过x块玻璃以后强度为y.
(1)写出y关于x的函数关系式;
(2)通过多少块玻璃以后,光线强度将减弱到原来的以下.(lg3≈0.477 1)
已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.