已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.
已知坐标平面内O为坐标原点,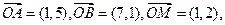 P是线段OM上一个动点.当
P是线段OM上一个动点.当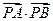 取最小值时,求
取最小值时,求 的坐标,并求
的坐标,并求 的值
的值
若函数 .
.
⑴判断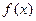 的奇偶性;
的奇偶性;
⑵当 时,判断
时,判断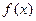 在
在 上的单调性,并加以证明
上的单调性,并加以证明
已知 ,设
,设 .
.
(1)求函数 的最小正周期,并写出
的最小正周期,并写出 的减区间;
的减区间;
(2)当 时,求函数
时,求函数 的最大值及最小值
的最大值及最小值
已知函数f ( x )=x 2+ax+b
(1)若对任意的实数x都有f (1+x)="f" (1-x) 成立,求实数 a的值;
(2)若f (x)为偶函数,求实数a的值;
(3)若f (x)在[ 1,+∞)内递增,求实数a的范围
设函数f(x)=loga(x-3a),g(x)=loga ,(a>0且a≠1).
,(a>0且a≠1).
(1)若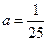 ,当
,当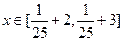 时,求证:|f(x)-g(x)|
时,求证:|f(x)-g(x)|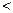 1;
1;
(2)当x∈[a+2,a+3]时,恒有|f(x)-g(x)| 1,试确定a的取值范围.
1,试确定a的取值范围.