设函数f(x)=loga(x-3a),g(x)=loga ,(a>0且a≠1).
,(a>0且a≠1).
(1)若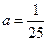 ,当
,当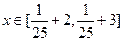 时,求证:|f(x)-g(x)|
时,求证:|f(x)-g(x)|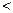 1;
1;
(2)当x∈[a+2,a+3]时,恒有|f(x)-g(x)| 1,试确定a的取值范围.
1,试确定a的取值范围.
(本小题满分12分)
已知数列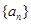 是公差不为零的等差数列,
是公差不为零的等差数列,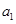 =1,且
=1,且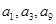 成等比数列.
成等比数列.
(1)求数列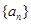 的通项;
的通项;
(2)设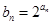 ,求数列
,求数列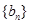 的前n项和Sn.
的前n项和Sn.
(本小题满分12分)
(1) 求不等式的解集:
(2)求函数的定义域:
定义在 上的函数
上的函数 满足:①
满足:① ,②对任意实数b,
,②对任意实数b,  .
.
(1)求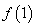 ,
,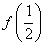 ,
, 及满足
及满足 的k值;
的k值;
(2)证明对任意 ,
, .
.
(3)证明 是
是 上的增函数.
上的增函数.
已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函数f(x)的表达式;
(Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.
设 是奇函数,
是奇函数, 是偶函数,并且
是偶函数,并且 ,求
,求 和
和 表达式。
表达式。