2008年中国北京奥运会吉祥物由5个“中国福娃”组成,分别叫贝贝、晶晶、欢欢、迎迎、妮妮.现有8个相同的盒子,每个盒子中放一只福娃,每种福娃的数量如下表:
| 福娃名称 |
贝贝 |
晶晶 |
欢欢 |
迎迎 |
妮妮 |
| 数量 |
1 |
1 |
1 |
2 |
3 |
从中随机地选取5只.(I)求选取的5只恰好组成完整“奥运吉祥物”的概率;
(II)若完整地选取奥运会吉祥物记10分;若选出的5只中仅差一种记8分;差两种记6分;以此类推. 设ξ表示所得的分数,求ξ的分布列及数学期望.
(本小题12分)
已知数列{an}中,a1="1" ,a2=3,且点(n,an)满足函数y = kx + b. (1)求k,b的值,并写出数列{an}的通项公式;
(1)求k,b的值,并写出数列{an}的通项公式;
(2)记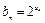 ,求数列{bn}的前n和Sn.
,求数列{bn}的前n和Sn.
(本小题10分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x米,总费用为y(单位:元).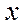
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,
并求出最小总费用.
(本小题10分)在△ABC中,角A,B,C的对边分别为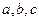 ,且满足
,且满足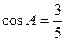 ,
,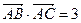 .
.
(1)求△ABC的面积.
(2)若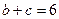 ,求
,求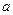 的值.
的值.
((本小题12分)
已知指数函数 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为 的函数
的函数 是奇函数。
是奇函数。
(1)确定 的解析式;
的解析式;
(2)求m,n的值;
(3)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
((本小题12分)
如图, 在三棱柱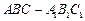 中,
中, 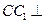 底面
底面 ,
,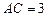 ,
, 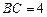 ,
,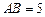 , 点D是
, 点D是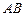 的中点.
的中点.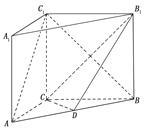
(1) 求证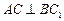 ;
;
(2) 求证 平
平 面
面