(本小题10分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x米,总费用为y(单位:元).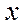
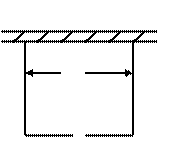
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,
并求出最小总费用.
设a,b,c R,a+b+c=0,abc=1.
(1)证明:ab+bc+ca<0;
(2)用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c}≥ .
在直角坐标系xOy中,曲线C的参数方程为 (t为参数且t≠1),C与坐标轴交于A、B两点.
(1)求 ;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求直线AB的极坐标方程.
设函数 ,曲线 在点( ,f( ))处的切线与y轴垂直.
(1)求b.
(2)若 有一个绝对值不大于1的零点,证明: 所有零点的绝对值都不大于1.
已知椭圆 的离心率为 , , 分别为 的左、右顶点.
(1)求 的方程;
(2)若点 在 上,点 在直线 上,且 , ,求 的面积.
如图,在长方体 中,点 分别在棱 上,且 , .
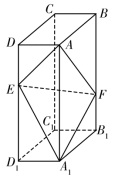
(1)证明:点 在平面 内;
(2)若
,
, 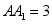 ,求二面角
的正弦值.
,求二面角
的正弦值.