建造一个容量为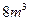 ,深度为
,深度为 的长方体无盖水池,如果池底和池壁的造价每平方分别为180元和80元,求水池的最低总造价。并求此时水池的长和宽。
的长方体无盖水池,如果池底和池壁的造价每平方分别为180元和80元,求水池的最低总造价。并求此时水池的长和宽。
已知抛物线
 的焦点为
的焦点为 ,抛物线上存在一点
,抛物线上存在一点 到焦点的距离为
到焦点的距离为 ,且点
,且点 在圆
在圆
 上.
上.
(1)求抛物线 的方程;
的方程;
(2)已知椭圆
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且离心率为
的焦点重合,且离心率为 .直线
.直线 交椭圆
交椭圆 于
于 、
、 两个不同的点,若原点
两个不同的点,若原点 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求 的取值范围.
的取值范围.
如图,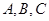 是椭圆
是椭圆
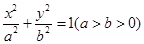 上的三点,其中点
上的三点,其中点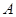 是椭圆的右顶点,
是椭圆的右顶点,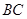 过椭圆
过椭圆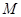 的中心,且满足
的中心,且满足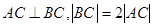 。
。
(1)求椭圆的离心率;
(2)若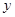 轴被
轴被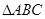 的外接圆所截得弦长为9,求椭圆方程。
的外接圆所截得弦长为9,求椭圆方程。
已知抛物线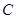 的顶点在坐标原点
的顶点在坐标原点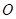 ,对称轴为
,对称轴为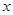 轴,焦点为
轴,焦点为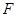 ,抛物线上一点
,抛物线上一点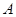 的横坐标为
的横坐标为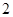 ,且
,且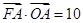 .
.
(1)求此抛物线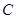 的方程;
的方程;
(2)过点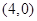 做直线
做直线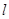 交抛物线
交抛物线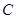 于
于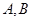 两点,求证:
两点,求证: .
.
在直角坐标系中,圆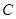 的参数方程
的参数方程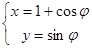 (
(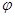 为参数).以
为参数).以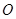 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线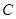 的极坐标方程;
的极坐标方程;
(2)设直线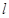 极坐标方程是
极坐标方程是 射线
射线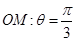 与圆
与圆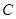 的交点为
的交点为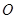 、
、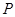 ,与直线
,与直线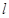 的交点为
的交点为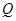 ,求线段
,求线段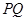 的长.
的长.
已知曲线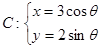 (
(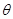 为参数)在同一直角坐标系中,将曲线
为参数)在同一直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线 ,
,
(1)求曲线 的普通方程;
的普通方程;
(2)若点 在曲线
在曲线 上,点
上,点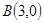 ,当
,当 在曲线
在曲线 上运动时,求
上运动时,求 中点
中点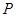 的轨迹方程。
的轨迹方程。